/Szkoła średnia/Geometria/Stereometria/Ostrosłup/Prawidłowy czworokątny/Objętość

Zadanie nr 7912529

Podstawa ostrosłupa prawidłowego czworokątnego ma pole 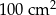2 100 cm , a jego pole powierzchni bocznej jest równe 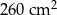260 cm 2 . Oblicz objętość tego ostrosłupa.

Wersja PDF

Rozwiązanie

Szkicujemy ostrosłup.

PIC

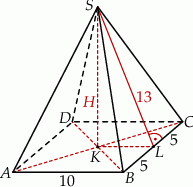
W podstawie ostrosłupa prawidłowego czworokątnego jest kwadrat o boku 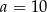a = 10 . Pole jednej ściany bocznej jest równe

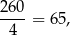
26-0 = 65, 4

więc jeżeli oznaczymy przez 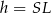h = SL wysokość ściany bocznej, to mamy

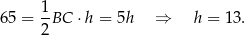
65 = 1BC ⋅h = 5h ⇒ h = 13. 2

Z twierdzenia Pitagorasa w trójkącie 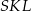SKL mamy

∘ ----------- ∘ --------- √ --------- √ ---- H = SL 2 − KL 2 = 1 32 − 5 2 = 169 − 25 = 144 = 12.

Objętość ostrosłupa jest więc równa

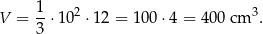
1- 2 3 V = 3 ⋅10 ⋅12 = 10 0⋅4 = 400 cm .

 
Odpowiedź: 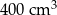400 cm 3 .

Wersja PDF