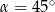/Szkoła średnia/Geometria/Stereometria/Ostrosłup/Prawidłowy czworokątny/Objętość

Zadanie nr 8071498

Podstawą ostrosłupa prawidłowego 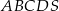ABCDS jest kwadrat 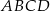ABCD . Punkt 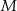M jest środkiem odcinka 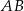AB , a punkt 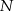N jest środkiem odcinka 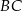BC . Trójkąt 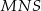MNS jest równoboczny i jego bok ma długość 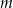m . Oblicz objętość ostrosłupa 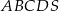ABCDS i kąt nachylenia ściany bocznej do płaszczyzny podstawy tego ostrosłupa.

Wersja PDF

Rozwiązanie

Zacznijmy od rysunku.

PIC

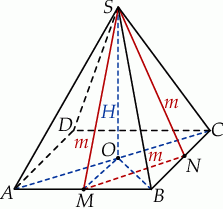
Odcinek 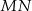MN jest odcinkiem łączącym środki boków w trójkącie 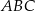ABC , więc jeżeli oznaczymy przez a długość boku kwadratu w podstawie ostrosłupa, to

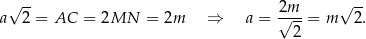
√ -- 2m-- √ -- a 2 = AC = 2MN = 2m ⇒ a = √ 2-= m 2.

Piszemy teraz twierdzenie Pitagorasa w trójkącie prostokątnym 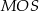MOS .

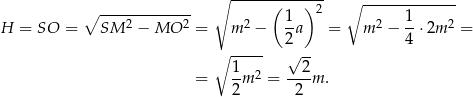
∘ ------------- ∘ ------------- ( ) 2 ∘ ------------- H = SO = SM 2 − MO 2 = m 2 − 1a = m 2 − 1-⋅2m 2 = 2 4 ∘ ----- √ -- = 1-m 2 = --2m . 2 2

Objętość ostrosłupa jest więc równa

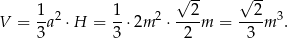
√ -- √ -- 1 1 2 2 V = --a2 ⋅H = --⋅2m 2 ⋅---m = ---m 3. 3 3 2 3

Kąt nachylenia ściany bocznej do płaszczyzny podstawy obliczamy z trójkąta 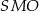SMO .

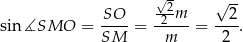
√2- √ -- sin ∡SMO = SO-- = -2-m- = --2. SM m 2

Zatem 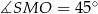∡SMO = 45 ∘ .  
Odpowiedź: 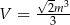√ - V = --2m3 3 , α = 45∘

Wersja PDF