/Szkoła średnia/Geometria/Stereometria/Ostrosłup/Prawidłowy czworokątny/Objętość

Zadanie nr 8897969

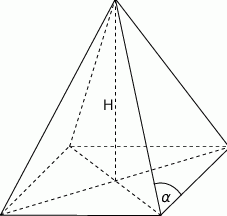
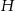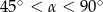W ostrosłupie prawidłowym czworokątnym dane są: H – wysokość ostrosłupa oraz α — miara kąta utworzonego przez krawędź boczną i krawędź podstawy (45∘ < α < 90∘ ).

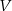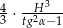  • Wykaż, że objętość V tego ostrosłupa jest równa 4⋅ -H-3-- 3 tg2α−1 .
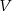  • Oblicz miarę kąta α , dla której objętość V danego ostrosłupa jest równa 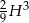2 3 9H . Wynik podaj w zaookrągleniu do całkowitej liczby stopni.
PIC
Wersja PDF

Rozwiązanie

PIC

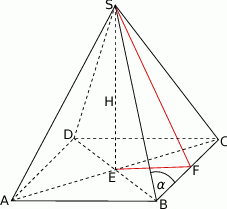
  • Ponieważ mamy daną wysokość ostrosłupa, wystarczy wyliczyć pole podstawy. Długość krawędzi podstawy możemy wyliczyć z trójkąta prostokątnego 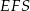EFS – jeden z jego boków jest równy połowie krawędzi podstawy, a drugi bok wyliczymy z trójkąta 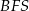BFS . Oznaczmy 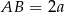AB = 2a (żeby nie mieć ułamków) i liczymy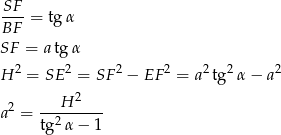
    SF- BF = tgα SF = a tg α H 2 = SE 2 = SF 2 − EF 2 = a2tg2 α− a2 2 a2 = ---H----- tg2α − 1

    Zatem objętość jest równa

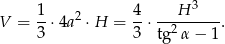
    1 4 H 3 V = --⋅4a 2 ⋅H = --⋅ --2-----. 3 3 tg α − 1
  • Musimy rozwiązać równanie
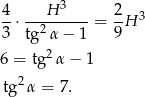
    4 H 3 2 --⋅---------= --H 3 3 tg2α − 1 9 6 = tg2α − 1 tg2α = 7.

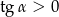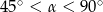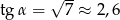    Ponieważ tg α > 0 (bo ∘ ∘ 45 < α < 90 ), więc √ -- tg α = 7 ≈ 2,6 . Miarę kąta α odczytujemy z tablic. ∘ α ≈ 69 .  
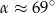    Odpowiedź: α ≈ 69∘

Wersja PDF