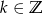Zadanie nr 1314257
Rozwiąż nierówność 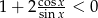 .
.
Rozwiązanie
Musimy założyć, że 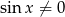 , czyli
, czyli 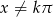 . Przekształcamy podaną nierówność
. Przekształcamy podaną nierówność
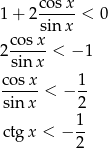
Rozwiązaniem tej nierówności są liczby 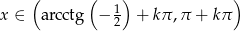 ,
, 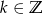 .
.
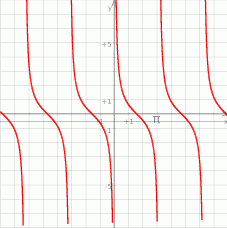
Odpowiedź: 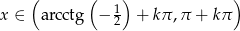 ,
, 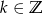
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Rozwiąż nierówność 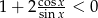 .
.
Musimy założyć, że 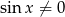 , czyli
, czyli 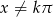 . Przekształcamy podaną nierówność
. Przekształcamy podaną nierówność
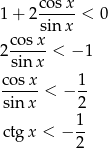
Rozwiązaniem tej nierówności są liczby 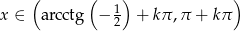 ,
, 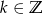 .
.

Odpowiedź: 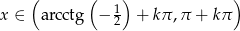 ,
,