Zadanie nr 5457974

Wyznaczyć obrazy zbiorów 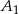A 1 i 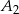oraz przeciwobraz zbioru 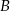przy funkcji 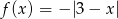f (x) = − |3− x| , jeżeli A1 = [− 2,3), A 2 = (− 2,5], B = (− ∞ ,− 3]∪ {0} .

Rozwiązanie

Sposób I

Startujemy od nierówności 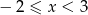− 2 ≤ x < 3 i sprawdzamy co z tą nierównością zrobi funkcja .

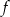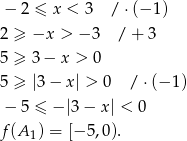
− 2 ≤ x < 3 / ⋅(− 1) 2 ≥ −x > − 3 / + 3 5 ≥ 3 − x > 0 5 ≥ |3 − x| > 0 / ⋅(− 1) − 5 ≤ − |3− x| < 0 f(A 1) = [− 5,0).

W przypadku zbioru 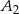postępujemy analogicznie.

− 2 < x ≤ 5 / ⋅(− 1) 2 > −x ≥ − 5 / + 3 5 > 3− x ≥ − 2 5 > |3 − x| ≥ 0 / ⋅(− 1) − 5 < |3 − x| ≤ 0 f(A 2) = (− 5,0 ].

Przeciwobraz 0 znajdujemy łatwo:

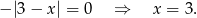
− |3 − x| = 0 ⇒ x = 3.

Przeciwobraz przedziału (− ∞ ,− 3 ] znajdujemy podobnie jak poprzednio, ale startujemy od końca.

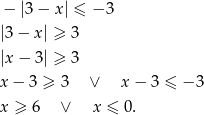
− |3− x | ≤ −3 |3− x| ≥ 3 |x− 3| ≥ 3 x − 3 ≥ 3 ∨ x− 3 ≤ − 3 x ≥ 6 ∨ x ≤ 0.

Zatem

−1 f (B ) = (− ∞ ,0]∪ {3} ∪ [6 + ∞ ).

Sposób II

Możemy łatwo naszkicować wykres danej funkcji: ponieważ 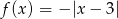f(x) = −|x − 3| , jest to wykres 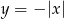y = − |x| przesunięty o 3 jednostki w prawo.

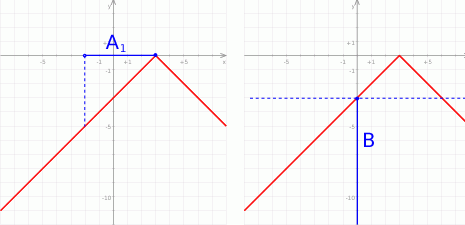
Z wykresu łatwo odczytać szukane zbiory.
Odpowiedź: f (A ) = [− 5,0),f (A 2) = (− 5,0],f −1(B ) = (− ∞ ,0]∪ {3} ∪ [6+ ∞ ) 1