Zadanie nr 4452847
Oblicz 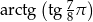 .
.
Rozwiązanie
Na początku przypomnijmy, że 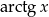 to odpowiedź na pytanie, gdzie tangens równa się
to odpowiedź na pytanie, gdzie tangens równa się  (jest to funkcja odwrotna do funkcji tangens). Oczywiście dla każdego
(jest to funkcja odwrotna do funkcji tangens). Oczywiście dla każdego  jest nieskończenie wiele takich odpowiedzi (tangens jest okresowy), więc trzeba ustalić jeden przedział, w którym szukamy odpowiedzi. Dla
jest nieskończenie wiele takich odpowiedzi (tangens jest okresowy), więc trzeba ustalić jeden przedział, w którym szukamy odpowiedzi. Dla 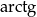 za taki przedział przyjmuje się
za taki przedział przyjmuje się 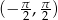 .
.
Musimy znaleźć kąt  w przedziale
w przedziale 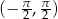 , dla którego
, dla którego 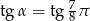 . Łatwo to zrobić z okresowości.
. Łatwo to zrobić z okresowości.
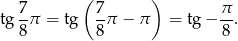
Zatem
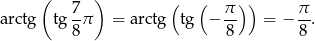
Odpowiedź: