/Szkoła średnia/Zadania maturalne/Matura 2008/Matura próbna
Próbny Egzamin Maturalny
z Matematyki poziom rozszerzony 7 marca 2008 Czas pracy: 180 minut
Suma trzech liczb rzeczywistych dodatnich jest równa 13. Druga liczba jest trzy razy większa od pierwszej. Wyznacz trzy liczby spełniające podane warunki tak, aby suma ich kwadratów była najmniejsza.
Na rysunku przedstawiono wykres pewnej funkcji wykładniczej 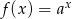 dla
dla 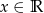
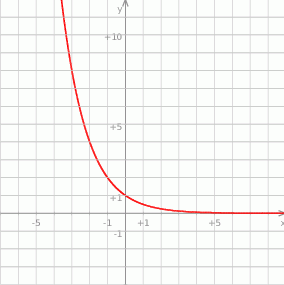
- Narysuj wykres funkcji
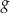 , który jest obrazem wykresu funkcji
, który jest obrazem wykresu funkcji 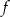 w przesunięciu o wektor
w przesunięciu o wektor ![→u = [2,− 1]](https://img.zadania.info/zes/0059844/HzesT5x.gif) .
. - Wyznacz
 i zapisz wzór funkcji
i zapisz wzór funkcji 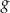 otrzymanej w wyniku tego przesunięcia.
otrzymanej w wyniku tego przesunięcia. - Odczytaj z wykresu zbiór wszystkich argumentów, dla których
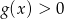 .
.
Wyznacz wszystkie wartości parametru 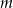 , dla których jedynym rozwiązaniem rzeczywistym równania
, dla których jedynym rozwiązaniem rzeczywistym równania 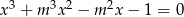 jest liczba 1.
jest liczba 1.
Wiadomo, że okrąg jest styczny do prostej o równaniu 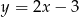 w punkcie
w punkcie 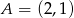 i styczny do prostej o równaniu
i styczny do prostej o równaniu 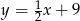 w punkcie
w punkcie 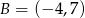 . Oblicz promień tego okręgu.
. Oblicz promień tego okręgu.
Narysuj wykres funkcji 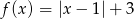 określonej dla
określonej dla 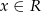 , a następnie na jego podstawie podaj liczbę rozwiązań równania
, a następnie na jego podstawie podaj liczbę rozwiązań równania 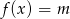 w zależności od parametru
w zależności od parametru 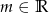 .
.
Właściciel sklepu z odzieżą kupił w hurtowni koszulki, płacąc za nie 720 zł. Gdyby każda koszulka kosztowała o 2 złote mniej, to za tę samą kwotę mógłby kupić o 5 koszulek więcej. Oblicz, ile koszulek kupił w tej hurtowni wspomniany właściciel sklepu. Podaj cenę jednej koszulki.
W czworokącie wypukłym 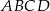 dane są:
dane są: 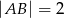 ,
, 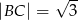 ,
, 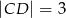 ,
, 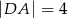 i
i 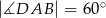 . Oblicz pole tego czworokąta.
. Oblicz pole tego czworokąta.
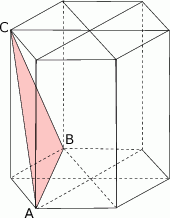
W graniastosłupie prawidłowym sześciokątnym płaszczyzna 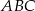 zawierająca przekątne sąsiednich ścian bocznych, wychodzących z tego samego wierzchołka, jest nachylona do podstawy graniastosłupa pod kątem
zawierająca przekątne sąsiednich ścian bocznych, wychodzących z tego samego wierzchołka, jest nachylona do podstawy graniastosłupa pod kątem 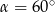 . Pole przekroju graniastosłupa tą płaszczyzną równa się
. Pole przekroju graniastosłupa tą płaszczyzną równa się 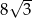 . Zaznacz na poniższym rysunku kąt
. Zaznacz na poniższym rysunku kąt  . Oblicz objętość tego graniastosłupa.
. Oblicz objętość tego graniastosłupa.
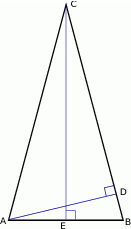
W trójkącie równoramiennym  , w którym
, w którym 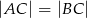 wysokość
wysokość 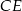 jest dwa razy dłuższa od wysokości
jest dwa razy dłuższa od wysokości 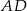 (patrz rysunek). Oblicz kosinusy wszystkich kątów wewnętrznych trójkąta
(patrz rysunek). Oblicz kosinusy wszystkich kątów wewnętrznych trójkąta 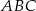 .
.
Ciąg geometryczny 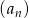 jest określony wzorem
jest określony wzorem 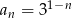 dla
dla 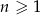 .
.
- Oblicz iloraz tego ciągu.
- Oblicz
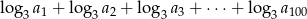 czyli sumę logarytmów, o podstawie 3, stu początkowych, kolejnych wyrazów tego ciągu.
czyli sumę logarytmów, o podstawie 3, stu początkowych, kolejnych wyrazów tego ciągu.
Rzucamy trzykrotnie symetryczną kostką sześcienną do gry. Oblicz prawdopodobieństwa następujących zdarzeń:
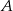 – na każdej kostce wypadnie nieparzysta liczba oczek,
– na każdej kostce wypadnie nieparzysta liczba oczek, 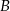 – suma kwadratów liczb wyrzuconych oczek będzie podzielna przez 3.
– suma kwadratów liczb wyrzuconych oczek będzie podzielna przez 3.

