Zadanie nr 1485852
Punkty 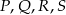 są środkami odpowiednio krawędzi
są środkami odpowiednio krawędzi 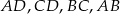 czworościanu
czworościanu 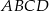 . Wykaż, że punkty
. Wykaż, że punkty 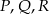 i
i 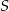 są wierzchołkami równoległoboku.
są wierzchołkami równoległoboku.
Rozwiązanie
Rozpoczynamy oczywiście od rysunku.
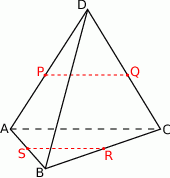
Zauważmy, że odcinek 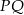 łączy środki boków w trójkącie
łączy środki boków w trójkącie 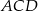 , czyli jest równoległy do krawędzi
, czyli jest równoległy do krawędzi 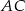 i
i 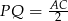 . Analogicznie, odcinek
. Analogicznie, odcinek 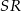 łączy środki boków w trójkącie
łączy środki boków w trójkącie 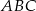 , czyli jest równoległy do
, czyli jest równoległy do 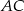 i
i 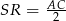 . W takim razie odcinki
. W takim razie odcinki 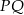 i
i 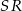 mają równe długości i są równoległe (bo oba są równoległe do
mają równe długości i są równoległe (bo oba są równoległe do 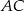 ), czyli czworokąt
), czyli czworokąt 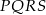 jest równoległobokiem.
jest równoległobokiem.

