Zadanie nr 2458445
Wykaż, że jeśli wszystkie krawędzie boczne ostrosłupa trójkątnego tworzą z podstawą kąty o równych miarach to spodek wysokości ostrosłupa jest środkiem okręgu opisanego na tym trójkącie.
Rozwiązanie
Zacznijmy od rysunku.
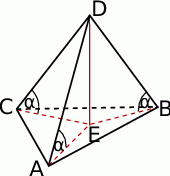
Jeżeli połączymy spodek wysokości 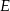 ostrosłupa z wierzchołkami podstawy, to mamy
ostrosłupa z wierzchołkami podstawy, to mamy
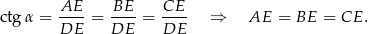
Zatem punkt 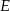 jest środkiem okręgu opisanego na trójkącie
jest środkiem okręgu opisanego na trójkącie 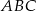 (jest równo odległy od wierzchołków).
(jest równo odległy od wierzchołków).

