Zadanie nr 3231435
Podstawą ostrosłupa 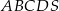 jest czworokąt wypukły
jest czworokąt wypukły 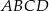 , w którym
, w którym 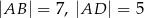 oraz
oraz 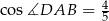 . Każda z krawędzi bocznych ostrosłupa ma długość
. Każda z krawędzi bocznych ostrosłupa ma długość 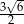 . Oblicz wysokość ostrosłupa.
. Oblicz wysokość ostrosłupa.
Rozwiązanie
Rozpoczynamy od szkicowego rysunku.
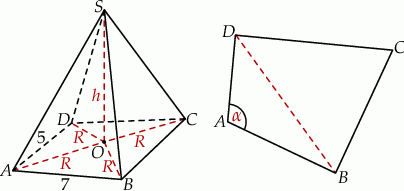
Zauważmy, że jeżeli 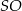 jest wysokością ostrosłupa to każdy z trójkątów
jest wysokością ostrosłupa to każdy z trójkątów 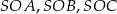 i
i 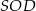 jest prostokątny i każde dwa z nich mają tę samą długość przeciwprostokątnej oraz jednej z przyprostokątnych (dokładnie:
jest prostokątny i każde dwa z nich mają tę samą długość przeciwprostokątnej oraz jednej z przyprostokątnych (dokładnie: 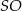 ). To oznacza, że trójkąty te są przystające, więc
). To oznacza, że trójkąty te są przystające, więc
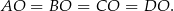
To z kolei oznacza, że na czworokącie 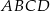 można opisać okrąg i punkt
można opisać okrąg i punkt 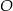 jest środkiem tego okręgu. W takim razie do obliczenia wysokości (np. z trójkąta
jest środkiem tego okręgu. W takim razie do obliczenia wysokości (np. z trójkąta 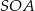 ) brakuje nam długości promienia okręgu opisanego na czworokącie
) brakuje nam długości promienia okręgu opisanego na czworokącie 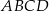 .
.
Zauważmy, że okrąg opisany na czworokącie 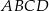 jest też okręgiem opisanym na trójkącie
jest też okręgiem opisanym na trójkącie 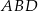 , więc jego promień możemy wyliczyć stosując twierdzenie sinusów w tym trójkącie. Tak się szczęśliwie składa, że mamy nawet podany
, więc jego promień możemy wyliczyć stosując twierdzenie sinusów w tym trójkącie. Tak się szczęśliwie składa, że mamy nawet podany 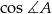 , więc do pełni szczęścia brakuje nam długości przekątnej
, więc do pełni szczęścia brakuje nam długości przekątnej 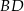 . Tę długość możemy jednak wyliczyć stosując twierdzenie cosinusów.
. Tę długość możemy jednak wyliczyć stosując twierdzenie cosinusów.
Wszystko wiemy, więc liczymy – na początek długość przekątnej 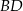 .
.
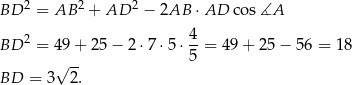
Teraz obliczamy 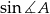
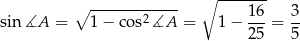
(sinus jest dodatni dla kątów wypukłych). Teraz piszemy twierdzenie sinusów w trójkącie 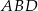 .
.
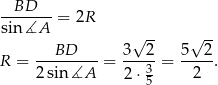
Teraz piszemy twierdzenie Pitagorasa w trójkącie 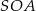 .
.
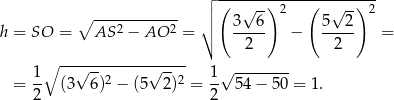
Odpowiedź: