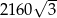/Szkoła średnia/Geometria/Stereometria/Ostrosłup/Dowolny

Zadanie nr 3942785

Dodaj do ulubionych
Dodaj do rozwiązanych

Podstawą ostrosłupa 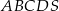ABCDS jest prostokąt o polu równym 432, a stosunek długości boków tego prostokąta jest równy 3:4. Przekątne podstawy 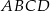ABCD przecinają się w punkcie 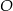O . Odcinek 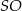SO jest wysokością ostrosłupa (zobacz rysunek). Kąt 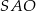SAO ma miarę 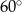6 0∘ . Oblicz objętość tego ostrosłupa.

PIC

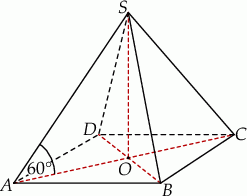
Rozwiązanie

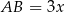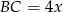Jeżeli oznaczymy AB = 3x i BC = 4x , to z podanego pola podstawy mamy

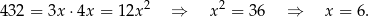
432 = 3x ⋅4x = 12x2 ⇒ x 2 = 36 ⇒ x = 6.

Wysokość ostrosłupa obliczymy z trójkąta prostokątnego 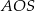AOS , ale zanim to zrobimy obliczmy długość odcinka AO .

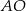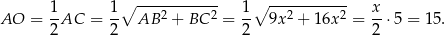
∘ ------------ ∘ ----------- AO = 1-AC = 1- AB 2 + BC 2 = 1- 9x 2 + 16x2 = x-⋅ 5 = 15. 2 2 2 2

Obliczamy teraz z trójkąta 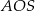AOS wysokość ostrosłupa.

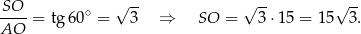
SO-- ∘ √ -- √ -- √ -- AO = tg 60 = 3 ⇒ SO = 3⋅1 5 = 15 3.

Pozostało obliczyć objętość ostrosłupa.

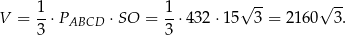
-- -- V = 1-⋅P ⋅SO = 1-⋅432 ⋅15√ 3 = 2160√ 3. 3 ABCD 3

 
Odpowiedź: √ -- 216 0 3

Wersja PDF