Zadanie nr 5259453
Podstawą ostrosłupa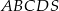 
jest romb o boku długości 6. Krawędź boczna 
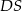ma długość 8 i jest jednocześnie wysokością tego ostrosłupa. Długości pozostałych trzech krawędzi bocznych są równe (zobacz rysunek).
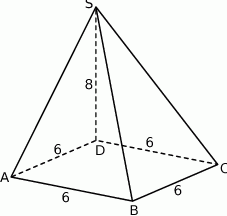
Oblicz objętość tego ostrosłupa.
Rozwiązanie
Trójkąt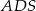 
jest prostokątny, więc
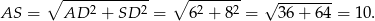
Zauważmy teraz, że trójkąt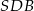 
też jest prostokątny oraz ma dwa boki tej samej długości, co trójkąt 
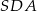. To oznacza, że te dwa trójkąty prostokątne są przystające i
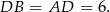
To z kolei oznacza, że romb w podstawie ostrosłupa składa się z dwóch trójkątów równobocznych i jego pole jest równe
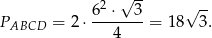
Objętość ostrosłupa jest więc równa
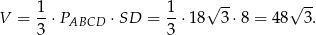
Odpowiedź: 
