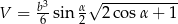/Szkoła średnia/Geometria/Stereometria/Ostrosłup/Dowolny

Zadanie nr 5927816

Dodaj do ulubionych
Dodaj do rozwiązanych

W ostrosłupie trójkątnym wszystkie krawędzie boczne i dwie krawędzie podstawy mają długość b , a kąt między równymi bokami podstawy ma miarę α . Oblicz objętość tego ostrosłupa.

Rozwiązanie

Zaczynamy od rysunku.

PIC

Z trójkąta prostokątnego ABF możemy łatwo wyliczyć długości odcinków FA i F B .

FA--= sin α- ⇒ FA = b sin α- AB 2 2 F B α α ----= cos -- ⇒ F B = bcos -. AB 2 2

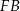Zatem pole podstawy 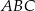ABC jest równe

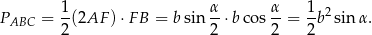
1- α- α- 1-2 PABC = 2(2AF )⋅F B = b sin 2 ⋅b cos 2 = 2b sin α.

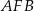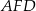Aby obliczyć wysokość ostrosłupa zauważmy, że trójkąty AF B i AF D są przystające, zatem 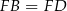F B = FD i trójkąt 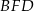BF D jest równoramienny. Znamy jego boki oraz łatwo możemy wyliczyć jego wysokość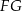 F G

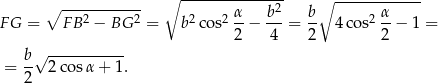
∘ ----------- ∘ -------------2- ∘ ------------ FG = F B2 − BG 2 = b2cos2 α-− b-= b- 4co s2 α-− 1 = 2 4 2 2 b√ ----------- = -- 2cos α+ 1. 2

Skoro znamy boki trójkąta i jedną z wysokości, to porównując dwa wzory na pole możemy wyliczyć drugą wysokość.

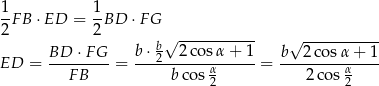
1 1 -F B ⋅ED = -BD ⋅FG 2 2 √ ----------- √ ----------- BD-⋅-FG-- b-⋅ b2-2-cos-α+--1 b---2cos-α+--1 ED = F B = b cos α = 2co s α 2 2

No i możemy policzyć objętość

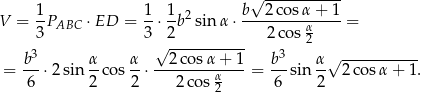
----------- 1 1 1 b√ 2cos α+ 1 V = -PABC ⋅ED = --⋅-b 2sinα ⋅---------α---- = 3 3√ 2---------- 2co s2 b3 α α 2 cos α+ 1 b3 α√ ----------- = ---⋅2 sin --cos --⋅---------α--- = ---sin -- 2 cosα + 1. 6 2 2 2 cos 2 6 2

 
Odpowiedź: 3 √ ----------- V = b6 sin α2 2 cos α+ 1

Wersja PDF