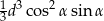/Szkoła średnia/Geometria/Stereometria/Ostrosłup/Dowolny

Zadanie nr 6141364

Dodaj do ulubionych
Dodaj do rozwiązanych

Podstawą ostrosłupa jest równoramienny trójkąt prostokątny. Każda krawędź boczna ma długość 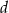d i jest nachylona do płaszczyzny podstawy pod kątem α . Oblicz objętość tego ostrosłupa.

Rozwiązanie

Jak to w zadaniach ze stereometrii zaczynamy od dużego rysunku.

PIC

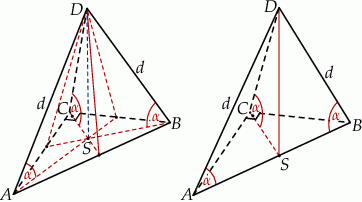
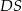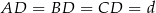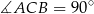Przyjmijmy oznaczenia z (lewego) rysunku, tzn. niech DS będzie wysokością ostrosłupa, AD = BD = CD = d oraz ∡ACB = 90∘ . Najważniejszą (i najtrudniejszą) rzeczą do zrobienia jest ustalenie, gdzie leży rzut wierzchołka 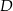D na płaszczyznę podstawy – jeżeli to ustalimy, to mając 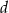d i α będziemy mogli zacząć liczyć długości odcinków w trójkącie ABC .

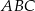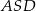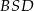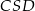Zauważmy, że trójkąty prostokątne ASD , BSD i CSD są przystające (mają takie same przeciwprostokątne i wspólną przyprostokątną). Zatem

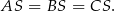
AS = BS = CS .

Oznacza to, że 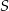S jest środkiem okręgu opisanego na trójkącie 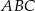ABC . Ale środek okręgu opisanego na trójkącie prostokątnym, to dokładnie środek przeciwprostokątnej. Zatem 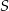S to środek krawędzi 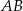AB i płaszczyzna 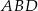ABD jest prostopadła do płaszczyzny podstawy (prawy rysunek).

Teraz wszystko jest już proste. Wysokość 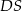DS ostrosłupa i wysokość 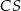CS trójkąta 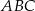ABC obliczamy z trójkąta prostokątnego CSD .

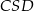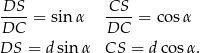
-DS- = sin α CS--= cosα DC DC DS = dsinα CS = dco sα.

Pozostało obliczyć długość przeciwprostokątnej trójkąta 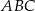ABC – liczymy to z trójkąta prostokątnego BSD .

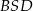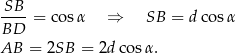
SB ----= cosα ⇒ SB = dco sα BD AB = 2SB = 2d cos α.

Stąd

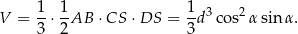
1 1 1 3 2 V = 3 ⋅ 2AB ⋅CS ⋅ DS = 3-d cos αsin α.

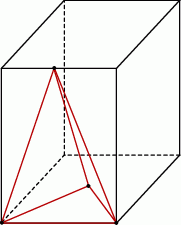
Jeżeli ktoś zastanawia się czy to możliwe, żeby istniał ostrosłup spełniający warunki zadania, to polecam uwadze kolejny rysunek, który pokazuje jak taki ostrosłup skonstruować w prostopadłościanie, który w podstawie ma kwadrat.

PIC

 
Odpowiedź: 13d 3cos2 αsin α

Wersja PDF