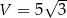Zadanie nr 8925501
Podstawą ostrosłupa 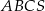 jest trójkąt
jest trójkąt 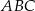 , w którym
, w którym 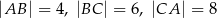 . Wszystkie ściany boczne tworzą z płaszczyzną podstawy kąt
. Wszystkie ściany boczne tworzą z płaszczyzną podstawy kąt 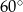 . Oblicz objętość ostrosłupa.
. Oblicz objętość ostrosłupa.
Rozwiązanie
Rozpoczynamy oczywiście od dużego rysunku.
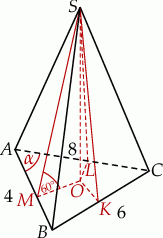
Na rysunku narysowaliśmy wysokości ścian bocznych, żeby móc zaznaczyć kąty nachylenia tych ścian do płaszczyzny podstawy. Ponieważ wszystkie ściany boczne są nachylone do płaszczyzny podstawy pod tym samym kątem, trójkąty prostokątne 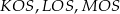 są przystające, czyli
są przystające, czyli 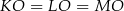 , co oznacza, że spodek wysokości
, co oznacza, że spodek wysokości 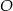 jest środkiem okręgu wpisanego w trójkąt
jest środkiem okręgu wpisanego w trójkąt 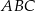 . W takim razie do wyliczenia długości wysokości
. W takim razie do wyliczenia długości wysokości 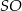 ostrosłupa brakuje nam długości promienia okręgu wpisanego w trójkąt
ostrosłupa brakuje nam długości promienia okręgu wpisanego w trójkąt 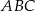 (bo wtedy skorzystamy z podanego kąta
(bo wtedy skorzystamy z podanego kąta 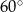 w trójkącie
w trójkącie 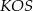 ). Długość promienia okręgu wpisanego możemy obliczyć ze wzoru
). Długość promienia okręgu wpisanego możemy obliczyć ze wzoru 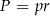 na pole trójkąta. Najpierw musimy jednak obliczyć to pole. Zrobimy to na dwa sposoby.
na pole trójkąta. Najpierw musimy jednak obliczyć to pole. Zrobimy to na dwa sposoby.
Sposób I
Korzystamy ze wzoru Herona na pole trójkąta
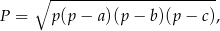
gdzie 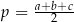 jest połową obwodu. W naszej sytuacji mamy
jest połową obwodu. W naszej sytuacji mamy
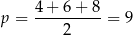
i pole jest równe
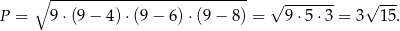
Możemy teraz obliczyć promień okręgu wpisanego.
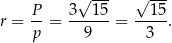
Obliczamy teraz wysokość
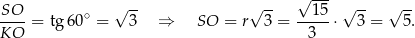
Pozostało obliczyć objętość.
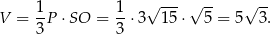
Sposób II
Pole trójkąta w podstawie możemy też obliczyć ze wzoru z sinusem, ale najpierw musimy obliczyć sinus jednego z kątów tego trójkąta. Robimy to przy pomocy twierdzenia cosinusów.
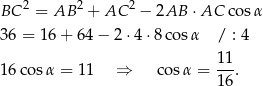
Zatem
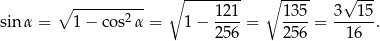
W takim razie pole trójkąta 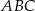 jest równe
jest równe
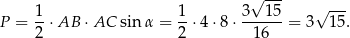
Promień okręgu wpisanego oraz wysokość i objętość ostrosłupa liczymy tak samo jak w pierwszym sposobie.
Odpowiedź: