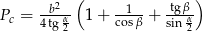/Szkoła średnia/Geometria/Stereometria/Ostrosłup/Dowolny

Zadanie nr 9800572

Dodaj do ulubionych
Dodaj do rozwiązanych

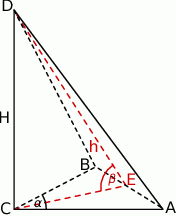
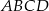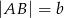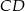Podstawą ostrosłupa ABCD jest trójkąt równoramienny o podstawie |AB | = b i kącie α pomiędzy ramionami. Krawędź CD jest wysokością ostrosłupa, a kąt nachylenia ściany 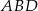ABD do podstawy ostrosłupa jest równy 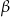β . Oblicz objętość i pole powierzchni całkowitej tego ostrosłupa.

Rozwiązanie

Niech 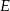E będzie środkiem krawędzi AB .

PIC

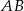W trójkącie prostokątnym 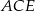ACE mamy

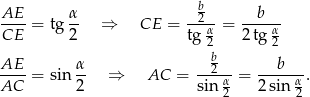
b AE-- α- -2-- --b--- CE = tg 2 ⇒ CE = tg α = 2tg α 2b 2 AE-- α- --2-- ---b--- AC = sin 2 ⇒ AC = sin α = 2 sin α . 2 2

W takim razie pole podstawy ostrosłupa jest równe

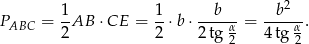
1 1 b b2 PABC = --AB ⋅ CE = --⋅b ⋅----α-= ----α-. 2 2 2 tg 2 4tg 2

Patrzymy teraz na trójkąt prostokątny 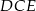DCE

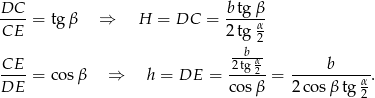
DC-- = tg β ⇒ H = DC = b-tgβ- CE 2 tg α2 --b-- CE-- 2tg α2 -----b----- DE = co sβ ⇒ h = DE = cosβ = 2 cosβ tg α. 2

Objętość ostrosłupa jest więc równa

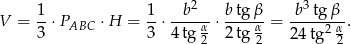
1 1 b2 btg β b3 tgβ V = --⋅PABC ⋅H = --⋅-----α⋅ ----α-= ------α. 3 3 4 tg 2 2tg 2 24tg2 2

Pole powierzchni całkowitej jest równe

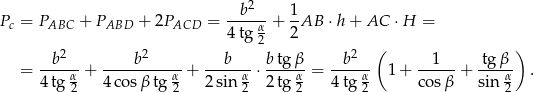
2 -b---- 1- Pc = PABC + PABD + 2PACD = 4tg α + 2 AB ⋅h + AC ⋅H = 2 2 2 2 ( ) = --b---+ ----b------+ ---b---⋅ btg-β-= -b---- 1 + --1--+ tg-β- . 4tg α2 4cos βtg α2 2 sin α2 2tg α2 4tg α2 cosβ sin α2

 
Odpowiedź: 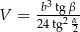b3tgβ V = 24tg2 α 2 , 2 ( tg β) Pc = 4btg α 1 + co1sβ + sin-α 2 2

Wersja PDF