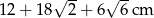/Szkoła średnia/Geometria/Planimetria/Trójkąt/Dowolny

Zadanie nr 1140058

Dodaj do ulubionych
Dodaj do rozwiązanych

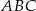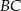W trójkącie ABC bok BC ma długość 12 cm. Oblicz obwód tego trójkąta, wiedząc, że miara kąta przy wierzchołku 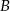B jest równa 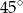4 5∘ , a miara kąta przy wierzchołku 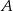A jest równa 30∘ .

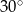Rozwiązanie

Zauważmy najpierw, że trzeci kąt trójkąta ma miarę 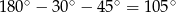∘ ∘ ∘ ∘ 180 − 3 0 − 45 = 105 .

PIC

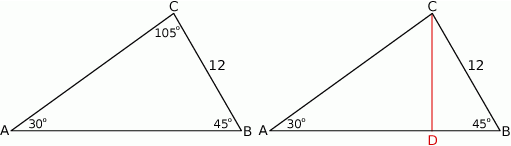
Sposób I

Będziemy chcieli skorzystać z twierdzenia sinusów, ale zanim to zrobimy, obliczmy 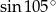sin 105∘ .

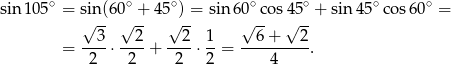
sin1 05∘ = sin(60∘ + 45∘) = sin 60∘ cos45 ∘ + sin 45∘co s60∘ = √ -- √ -- √ -- √ -- √ -- = --3-⋅ --2+ --2-⋅ 1-= --6-+---2. 2 2 2 2 4

Korzystamy teraz z twierdzenia sinusów.

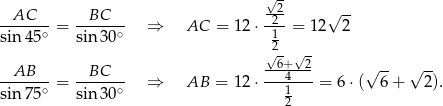
√ - --2 √ -- -AC----= --BC--- ⇒ AC = 12 ⋅-2- = 12 2 sin 45∘ sin3 0∘ 12 √ 6+ √2 --AB--- --BC--- ---4--- √ -- √ -- sin 75∘ = sin3 0∘ ⇒ AB = 12⋅ 1 = 6⋅ ( 6+ 2). 2

Obwód trójkąta jest więc równy

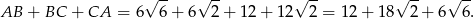
√ -- √ -- √ -- √ -- √ -- AB + BC + CA = 6 6 + 6 2 + 1 2+ 1 2 2 = 12 + 18 2+ 6 6.

Sposób II

Tym razem obejdziemy się bez twierdzenia sinusów. Dorysujmy wysokość 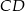CD trójkąta. Trójkąt 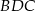BDC jest prostokątny z kątem ostrym 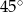4 5∘ , więc jest to połówka kwadratu. Mamy więc

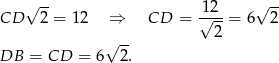
√ -- -12- √ -- CD 2 = 12 ⇒ CD = √ --= 6 2 √ -- 2 DB = CD = 6 2.

Patrzymy teraz na trójkąt ADC .

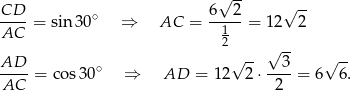
√ -- CD-- ∘ 6--2- √ -- AC = sin3 0 ⇒ AC = 1 = 1 2 2 2 √ -- AD ∘ √ -- 3 √ -- ---- = co s30 ⇒ AD = 12 2⋅ ----= 6 6. AC 2

Obwód trójkąta jest więc równy

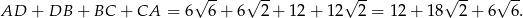
-- √ -- √ -- √ -- -- AD + DB + BC + CA = 6 √ 6+ 6 2+ 12+ 12 2 = 1 2+ 18 2+ 6√ 6.

 
Odpowiedź: √ -- √ -- 12 + 18 2+ 6 6 cm

Wersja PDF