/Szkoła średnia/Geometria/Planimetria/Trójkąt/Dowolny

Zadanie nr 1612048

Dodaj do ulubionych
Dodaj do rozwiązanych

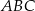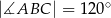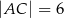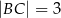W trójkącie ABC dane są kąt ∘ |∡ABC | = 12 0 , |AC | = 6 i |BC | = 3 . Dwusieczna kąta 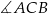∡ACB przecina bok 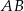AB w punkcie 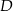D . Oblicz długość odcinka CD .

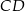Rozwiązanie

Zaczynamy od rysunku.

PIC

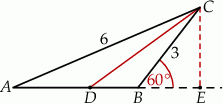
Plan jest prosty, najpierw obliczymy długość boku 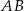AB , potem, z twierdzenia o dwusiecznej wyliczymy 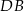DB . Na koniec, z twierdzenia cosinusów, wyliczymy CD .

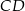Bok 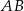AB można obliczyć na różne sposoby, np. pisząc twierdzenie cosinusów w trójkącie 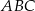ABC . Inny sposób, to poprowadzenie wysokości 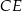CE i skorzystanie z definicji funkcji trygonometrycznych.

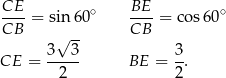
CE--= sin6 0∘ BE--= cos60 ∘ CB √ -- CB 3 3 3 CE = ----- BE = --. 2 2

Stąd

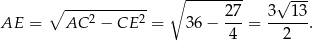
∘ -------- √ --- ∘ ------------ 27 3 1 3 AE = AC 2 − CE 2 = 36 − ---= ------. 4 2

Czyli 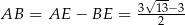3√13−3- AB = AE − BE = 2 . Na mocy twierdzenia o dwusiecznej,

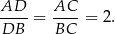
AD AC ---- = ---- = 2. DB BC

Zatem

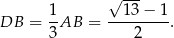
√ --- DB = 1AB = --13-−-1. 3 2

Stosujemy teraz twierdzenie cosinusów do trójkąta 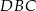DBC .

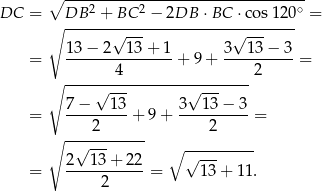
∘ ---2------2---------------------∘ DC = DB---+-BC--−--2DB--⋅BC-⋅-cos120- = ∘ √ --- √ --- 13-−-2--13-+-1- 3--13-−-3- = 4 + 9 + 2 = ∘ ----√------------√-------- 7 − 13 3 13− 3 = ---------+ 9 + ---------- = ∘ ----2------- 2 √ --- ∘ √--------- = 2--13-+-22-= 13 + 1 1. 2

 
Odpowiedź: ∘ √--------- 13+ 11

Wersja PDF