/Szkoła średnia/Geometria/Planimetria/Trójkąt/Dowolny

Zadanie nr 1955182

Dodaj do ulubionych
Dodaj do rozwiązanych

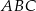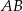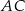W trójkącie ABC długości boków AB i AC są odpowiednio równe 4 i 6. Punkt 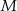M jest środkiem odcinka 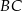BC , a długość środkowej 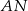AN trójkąta 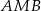AMB jest równa 3. Oblicz długość boku BC .

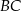Rozwiązanie

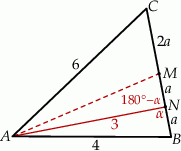
Zaczynamy od rysunku i oznaczmy 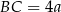BC = 4a .

PIC

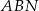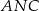Pomysł jest następujący – napiszemy twierdzenia cosinusów w trójkątach ABN i ANC . Ponieważ 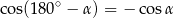cos(18 0∘ − α) = − co sα dodając te twierdzenia cosinusów stronami skrócimy składniki z α i to pozwoli nam obliczyć a . Liczymy

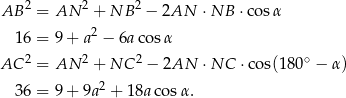
AB 2 = AN 2 + NB 2 − 2AN ⋅NB ⋅cos α 16 = 9+ a2 − 6a cos α 2 2 2 ∘ AC = AN + NC − 2AN ⋅NC ⋅cos(1 80 − α) 36 = 9+ 9a2 + 18aco sα.

Mnożymy pierwszą równość przez 3 i dodajemy do drugiej.

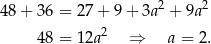
4 8+ 36 = 27 + 9 + 3a2 + 9a2 2 48 = 12a ⇒ a = 2.

Zatem 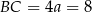BC = 4a = 8 .  
Odpowiedź: 8

Wersja PDF