/Szkoła średnia/Geometria/Planimetria/Trójkąt/Dowolny

Zadanie nr 1981335

Dodaj do ulubionych
Dodaj do rozwiązanych

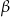Jeden z boków trójkąta ma długość c , zaś kąty trójkąta przyległe do tego boku mają miary α i β . Znajdź promień okręgu wpisanego w ten trójkąt.

Rozwiązanie

Zaczynamy od rysunku.

PIC

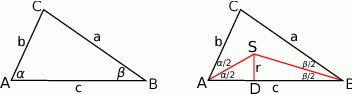
Sposób I

Aby wyznaczyć promień okręgu wpisanego w trójkąt będziemy chcieli skorzystać ze wzoru na pole 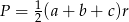P = 12(a + b + c)r . Aby to zrobić musimy najpierw wyliczyć pole i obwód danego trójkąta.

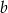Zacznijmy od wyliczenia długości boków a i b – zrobimy to z twierdzenia sinusów

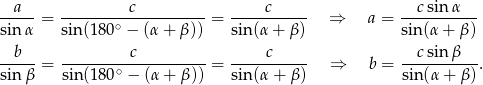
a c c csin α ----- = --------∘----------- = ----------- ⇒ a = ----------- sinα sin(18 0 − (α+ β)) sin (α+ β) sin (α+ β) --b-- ----------c--------- ----c------ --csin-β--- sinβ = sin(1 80∘ − (α+ β)) = sin (α+ β) ⇒ b = sin(α + β).

Mając długości boków łatwo wyliczamy pole

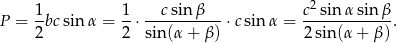
2 P = 1bc sin α = 1⋅ --csin-β---⋅csin α = c--sin-α-sin-β-. 2 2 sin (α+ β) 2 sin(α + β)

Pozostało policzyć promień okręgu wpisanego.

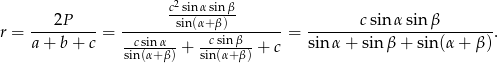
c2sinα sinβ ---2P---- -------sin(α+β)-------- -------csin-αsin-β-------- r = a + b + c = -csin-α-- --csinβ-- = sinα + sin β + sin(α + β). sin(α+β) + sin(α+ β) + c

Sposób II

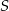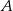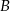Tym razem połączmy środek okręgu wpisanego S z wierzchołkami A i B trójkąta. Ponadto niech 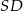SD będzie wysokością trójkąta 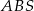ABS . Mamy zatem

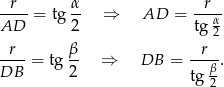
r α r AD--= tg 2- ⇒ AD = tg-α 2 -r-- β- -r-- DB = tg 2 ⇒ DB = β-. tg 2

Stąd

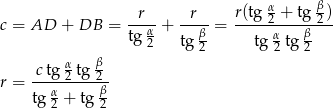
α β- c = AD + DB = -r--+ -r--= r(tg-2 +-tg-2-) tg α2 tg β- tg α tg β 2 2 2 ctg α2 tg β2- r = ---α------β- tg 2 + tg 2

 
Odpowiedź: β -----csinαsinβ---- = ctg α2 tg2 sinα+sin β+sin(α+ β) tg α2+tg β2

Wersja PDF