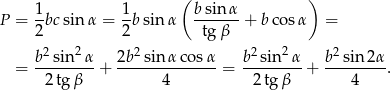Zadanie nr 2357921
W trójkącie 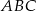 bok
bok 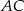 ma długość
ma długość 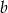 ,
, 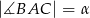 oraz
oraz 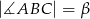 . Wykaż, że pole trójkąta
. Wykaż, że pole trójkąta 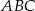 jest równe
jest równe
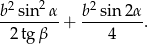
Rozwiązanie
Szkicujemy opisaną sytuację.
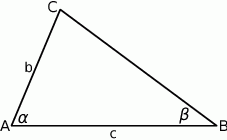
Pole trójkąta 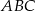 jest oczywiście równe
jest oczywiście równe
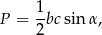
gdzie 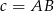 . Musimy więc tylko obliczyć
. Musimy więc tylko obliczyć  w zależności od
w zależności od 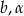 i
i 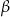 .
.
Na mocy twierdzenia sinusów mamy

Pole trójkąta 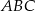 jest więc równe
jest więc równe