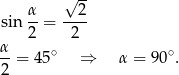/Szkoła średnia/Geometria/Planimetria/Trójkąt/Dowolny

Zadanie nr 2480708

Dodaj do ulubionych
Dodaj do rozwiązanych

Wykaż, że jeżeli kąty wewnętrzne trójkąta spełniają warunek 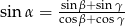sinβ+-sinγ- sin α = cosβ+ cos γ to trójkąt ten jest prostokątny.

Rozwiązanie

Zacznijmy od rysunku.

PIC

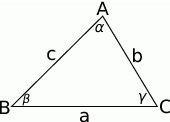
Sposób I

Na mocy twierdzeń sinusów i cosinusów mamy

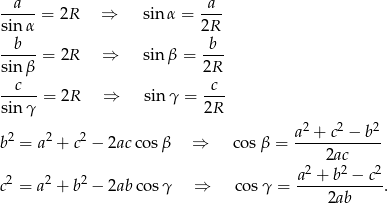
-a---= 2R ⇒ sinα = -a- sin α 2R -b--- -b- sin β = 2R ⇒ sinβ = 2R c c -----= 2R ⇒ sinγ = --- sin γ 2R a2 + c2 − b2 b 2 = a2 + c2 − 2ac cosβ ⇒ co sβ = ------------ 2ac 2 2 2 a2-+-b2 −-c2 c = a + b − 2ab cos γ ⇒ cosγ = 2ab .

Podany warunek możemy więc zapisać w postaci

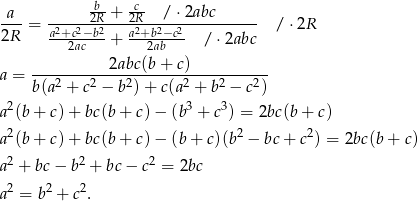
a-- ------b2R +-2cR---/⋅-2abc------ 2R = a2+c2−b2 a2+b2−c2 / ⋅2R 2ac + 2ab / ⋅2abc ----------2abc-(b+--c)----------- a = b(a2 + c2 − b2)+ c(a2 + b2 − c2) a2(b + c) + bc(b + c)− (b3 + c3) = 2bc(b + c) 2 2 2 a (b + c) + bc(b + c)− (b+ c)(b − bc+ c ) = 2bc(b+ c) a2 + bc − b2 + bc− c2 = 2bc 2 2 2 a = b + c .

Czyli trójkąt jest prostokątny.

Sposób II

Tym razem pozostaniemy w krainie trygonometrii. Mamy

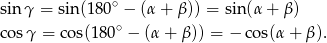
sin γ = sin (180∘ − (α + β)) = sin(α + β) ∘ cosγ = cos(18 0 − (α + β)) = − co s(α+ β).

Zatem dany warunek możemy zapisać w postaci:

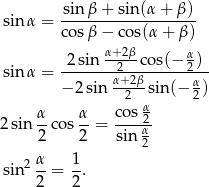
sinα = sin-β+--sin-(α+--β)- cos β− cos(α + β) α+2β- α sinα = -2sin---2--cos(−-2)-- − 2sin α+2β-sin (− α) 2 α 2 2sin α-cos α = co-s2- 2 2 sin α2 α 1 sin2 --= --. 2 2

Po drodze korzystaliśmy z ze wzorów na sumę sinusów, różnicę cosinusów i sinus podwojonego kąta. Pozostało skorzystać z tego, że α 2 jest kątem ostrym.

√ -- sin α-= ---2 2 2 α-= 45∘ ⇒ α = 9 0∘. 2
Wersja PDF