Zadanie nr 3264062
Pole trójkąta 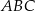 jest równe
jest równe 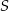 , a długości jego boków
, a długości jego boków 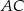 i
i 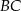 są odpowiednio równe
są odpowiednio równe 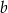 i
i  . Na bokach
. Na bokach 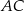 i
i 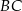 zbudowano kwadraty o środkach odpowiednio
zbudowano kwadraty o środkach odpowiednio 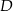 i
i 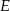 .
.
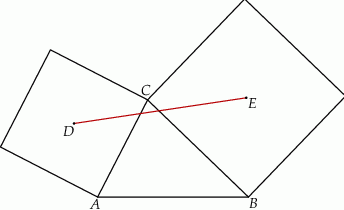
Wykaż, że
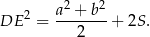
Rozwiązanie
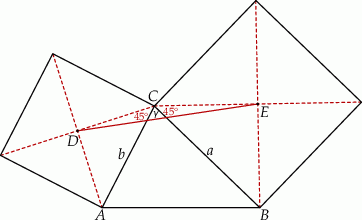
Dorysujmy przekątne kwadratów i oznaczmy 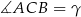 .
.
Piszemy twierdzenie cosinusów w trójkącie 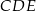 .
.