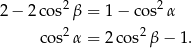/Szkoła średnia/Geometria/Planimetria/Trójkąt/Dowolny

Zadanie nr 3311630

Dodaj do ulubionych
Dodaj do rozwiązanych

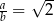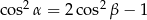Wykaż, że jeżeli w trójkącie a √ -- b = 2 to 2 2 cos α = 2 cos β − 1 .

PIC

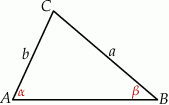
Rozwiązanie

Sposób I

Na mocy twierdzenia sinusów mamy

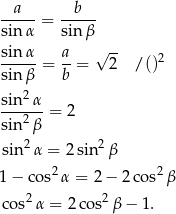
a b ----- = ----- sinα sin β sinα- a- √ -- 2 sinβ = b = 2 / () 2 sin-α- sin2β = 2 2 2 sin α = 2sin β 2 2 1− cos α = 2− 2cos β cos2 α = 2 cos2β − 1 .

Sposób II

Dorysujmy wysokość opuszczoną z wierzchołka 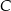C .

PIC

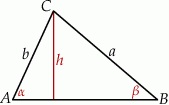
Mamy więc

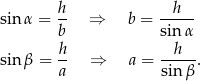
h- --h-- sin α = b ⇒ b = sin α h h sin β = -- ⇒ a = ----. a sin β

Podstawiamy teraz te wyrażenia do danej równości.

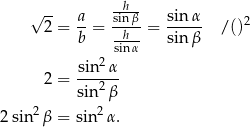
--h- √ -- a- sin-β sin-α- 2 2 = b = --h- = sin β /() sinα sin2-α 2 = 2 sin β 2sin2 β = sin2α .

Korzystamy teraz z jedynki trygonometrycznej.

2− 2cos2 β = 1 − cos2 α 2 2 co s α = 2 cos β − 1.
Wersja PDF