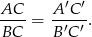Zadanie nr 3713257
Dane są dwa trójkąty: 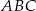 oraz
oraz 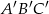 takie, że
takie, że 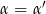 oraz
oraz 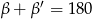 .
.
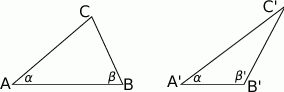
Wykaż, że:
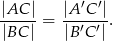
Rozwiązanie
Ponieważ
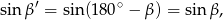
na mocy twierdzenia sinusów mamy
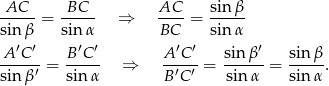
Zatem rzeczywiście
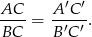
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Dane są dwa trójkąty: 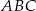 oraz
oraz 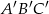 takie, że
takie, że 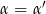 oraz
oraz 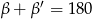 .
.

Wykaż, że:
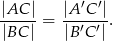
Ponieważ
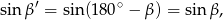
na mocy twierdzenia sinusów mamy
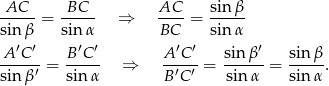
Zatem rzeczywiście