Zadanie nr 3934640
W trójkącie 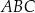 poprowadzono odcinki
poprowadzono odcinki 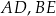 i
i 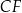 w ten sposób, że punkty
w ten sposób, że punkty 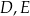 i
i 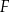 są środkami odpowiednio odcinków
są środkami odpowiednio odcinków 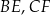 i
i 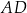 . Oblicz pole trójkąta
. Oblicz pole trójkąta 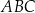 jeżeli pole trójkąta
jeżeli pole trójkąta 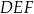 jest równe 2.
jest równe 2.
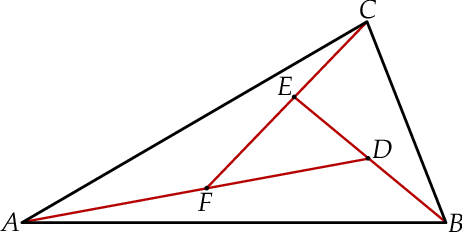
Rozwiązanie
Dorysujmy odcinki 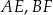 i
i 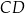 .
.
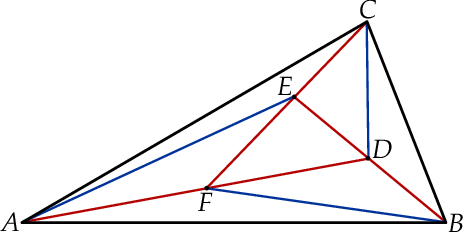
Zauważmy teraz, że każde dwa z utworzonych trójkątów mają równe pola.
Trójkąty 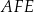 i
i 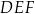 mają wspólną wysokość opuszczoną z
mają wspólną wysokość opuszczoną z 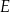 , więc
, więc
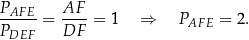
Trójkąty 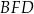 i
i 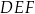 mają wspólną wysokość opuszczoną z
mają wspólną wysokość opuszczoną z 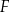 , więc
, więc
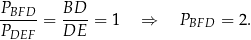
Trójkąty 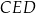 i
i 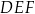 mają wspólną wysokość opuszczoną z
mają wspólną wysokość opuszczoną z 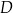 , więc
, więc
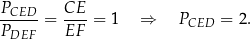
Analogicznie uzasadniamy, że
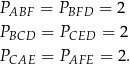
W takim razie
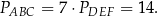
Odpowiedź: 14

