/Szkoła średnia/Geometria/Planimetria/Trójkąt/Dowolny

Zadanie nr 4229186

Dodaj do ulubionych
Dodaj do rozwiązanych

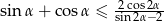Wykaż, że jeżeli trójkąt nie jest rozwartokątny, oraz miara α jednego z jego kątów spełnia warunek sin α + cos α ≤ s2icno2sα2−α2 to trójkąt ten jest prostokątny.

Rozwiązanie

Będziemy korzystać ze wzorów

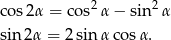
2 2 co s2α = cos α − sin α sin 2α = 2 sinα cos α.

Przekształcamy podaną nierówność

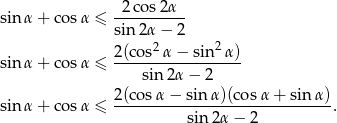
sinα + cosα ≤ -2co-s2α-- sin 2α − 2 2(cos2α − sin2 α) sinα + cosα ≤ ------------------ sin 2α − 2 2(cosα-−--sin-α)(cos-α+--sin-α)- sinα + cosα ≤ sin 2α − 2 .

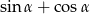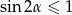Zauważmy teraz, że ponieważ trójkąt nie jest rozwartokątny, wyrażenie sin α + cos α jest dodatnie, więc możemy przez nie podzielić stronami. Zauważmy też, że mianownik ułamka z prawej strony nierówności jest ujemny, bo sin 2α ≤ 1 .

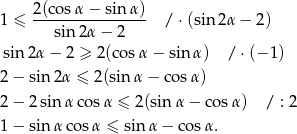
1 ≤ 2(co-sα-−-sinα-) / ⋅(sin2 α− 2) sin2α − 2 sin2 α− 2 ≥ 2(cos α− sin α) /⋅ (−1 ) 2− sin 2α ≤ 2 (sin α − cos α) 2− 2sinα cos α ≤ 2(sin α− cosα ) / : 2 1− sin α cosα ≤ sin α − cos α.

Dalszą część rozwiązania przeprowadzimy na dwa sposoby.

Sposób I

Przekształcamy dalej otrzymaną nierówność (wyłączamy 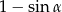1− sin α ).

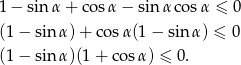
1 − sin α+ cosα − sin αco sα ≤ 0 (1 − sin α)+ cosα (1− sin α) ≤ 0 (1 − sin α)(1+ cosα ) ≤ 0.

Ponieważ trójkąt nie jest rozwartokątny, więc 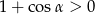1 + cos α > 0 i mamy

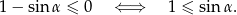
1− sin α ≤ 0 ⇐ ⇒ 1 ≤ sinα .

To oczywiście oznacza, że 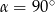α = 90∘ .

Sposób II

Chcielibyśmy podnieść nierówność stronami do kwadratu, w tym celu musimy założyć, że prawa strona jest nieujemna, czyli 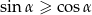sin α ≥ cos α . Przekształcamy dalej

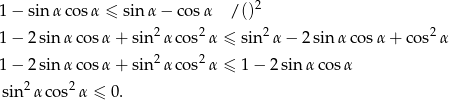
2 1 − sin αcos α ≤ sin α− cosα /() 1 − 2 sin α cosα + sin2 αco s2α ≤ sin2 α− 2sin αcos α+ cos2α 2 2 1 − 2 sin α cosα + sin αco s α ≤ 1 − 2 sin α cosα sin 2α cos2α ≤ 0.

W takim razie albo 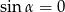sin α = 0 , co jest niemożliwe w trójkącie, albo 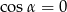cosα = 0 , co oznacza, że 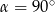α = 90∘ . Na koniec powinniśmy jeszcze sprawdzić, czy kąt ten spełnia zrobione po drodze założenie 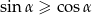sinα ≥ cosα – jest OK, bo 1>0.

Wersja PDF