/Szkoła średnia/Geometria/Planimetria/Trójkąt/Dowolny

Zadanie nr 4246560

Dodaj do ulubionych
Dodaj do rozwiązanych

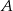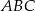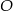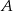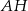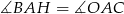Wierzchołek A trójkąta ostrokątnego ABC połączono odcinkiem ze środkiem O okręgu opisanego. Z wierzchołka A poprowadzono wysokość AH . Wykaż, że ∡BAH = ∡OAC .

Rozwiązanie

Oznaczmy 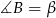∡B = β i połączmy środek okręgu z wierzchołkiem C .

PIC

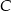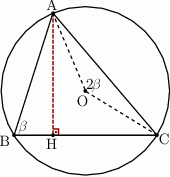
Kąt środkowy 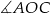∡AOC i kąt wpisany 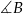∡B oparte są na tym samym łuku, więc

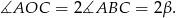
∡AOC = 2∡ABC = 2β.

Trójkąt AOC jest równoramienny, więc

180∘ −-2β- ∘ ∡OAC = 2 = 90 − β.

Teraz patrzymy na trójkąt prostokątny ABH .

∡BAH = 90∘ − ∡ABH = 90∘ − β .

Zatem istotnie 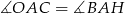∡OAC = ∡BAH .

Wersja PDF