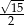Zadanie nr 4531573
Na trójkącie o bokach długości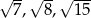 
opisano okrąg. Oblicz promień tego okręgu.
Rozwiązanie
Gdy przyjrzymy się podanym długościom boków, to bez problemu powinniśmy zauważyć, że dany trójkąt jest prostokątny.
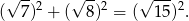
Szkicujemy trójkąt prostokątny.
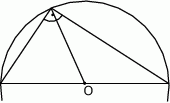
Zauważmy teraz, że okrąg o średnicy będącej przeciwprostokątną trójkąta to dokładnie okrąg opisany na trójkącie (bo kąt oparty na średnicy jest prosty). W takim razie promień tego okręgu to połowa przeciwprostokątnej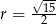 
.
Odpowiedź: 
