Zadanie nr 4631283
Dany jest trójkąt 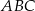 , w którym
, w którym 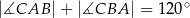 . Ponadto wiadomo, że
. Ponadto wiadomo, że 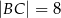 i
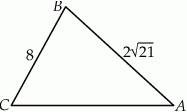
i 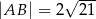 (zobacz rysunek). Oblicz długość trzeciego boku trójkąta
(zobacz rysunek). Oblicz długość trzeciego boku trójkąta 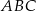 .
.
Rozwiązanie
Oczywiście
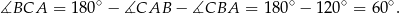
Sposób I
Dorysujmy wysokość 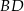 opuszczoną z wierzchołka
opuszczoną z wierzchołka 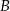 .
.
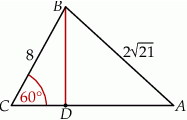
Trójkąt 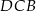 jest połówką trójkąta równobocznego o boku
jest połówką trójkąta równobocznego o boku 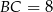 , więc
, więc 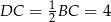 i
i
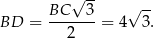
Z twierdzenia Pitagorasa w trójkącie 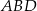 mamy
mamy
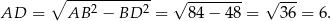
Stąd
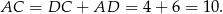
Sposób II
Jeżeli oznaczymy 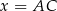 , to na mocy twierdzenia cosinusów mamy
, to na mocy twierdzenia cosinusów mamy
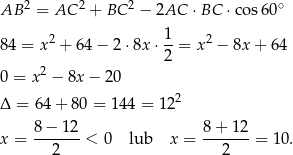
Zatem 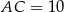 .
.
Odpowiedź: