Zadanie nr 4708666
Wiedząc, że punkt 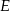 jest środkiem odcinka
jest środkiem odcinka 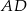 , a punkt
, a punkt 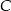 jest środkiem odcinka
jest środkiem odcinka 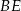 oraz
oraz 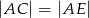 , wykaż, że
, wykaż, że 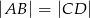 .
.
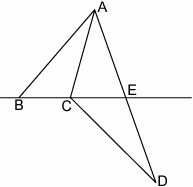
Rozwiązanie
Pokażemy, że trójkąty 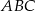 i
i 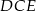 są przystające.
są przystające.
Rzeczywiście, z założenia
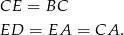
Ponadto
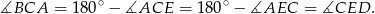
Trójkąty 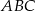 i
i 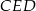 mają dwa równe boki, oraz taki sam kąt między tymi bokami, więc są przystające. Zatem
mają dwa równe boki, oraz taki sam kąt między tymi bokami, więc są przystające. Zatem 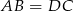 .
.

