Zadanie nr 6258844
Okrąg wpisany w trójkąt 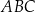 jest styczny do boków
jest styczny do boków 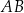 i
i 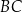 w punktach
w punktach 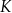 i
i 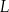 odpowiednio. Na bokach
odpowiednio. Na bokach 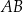 i
i 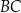 tego trójkąta wybrano punkty
tego trójkąta wybrano punkty 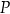 i
i 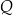 w ten sposób, że odcinek
w ten sposób, że odcinek 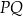 jest styczny do okręgu wpisanego w trójkąt
jest styczny do okręgu wpisanego w trójkąt 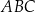 (zobacz rysunek).
(zobacz rysunek).

Wykaż, że jeżeli 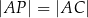 ,
, 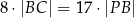 i
i 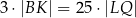 , to trójkąt
, to trójkąt 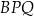 jest rozwartokątny.
jest rozwartokątny.
Rozwiązanie
Niech 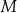 i
i 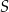 będą punktami styczności okręgu wpisanego w trójkąt
będą punktami styczności okręgu wpisanego w trójkąt 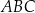 z odcinkami
z odcinkami 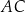 i
i 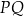 odpowiednio.
odpowiednio.

W rozwiązaniu kilkukrotnie skorzystamy z tego, że odcinki stycznych do okręgu poprowadzonych z jednego punktu mają równą długość. Taką sytuację mamy np. dla odcinków 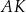 i
i 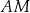 . W połączeniu z równością
. W połączeniu z równością 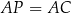 , otrzymujemy stąd
, otrzymujemy stąd
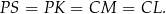
Oznaczmy tą wspólną długość przez  . Oznaczmy ponadto
. Oznaczmy ponadto
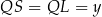
i 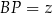 . Odcinki
. Odcinki 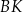 i
i 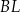 mają równą długość, więc
mają równą długość, więc
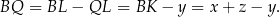
Teraz łatwo już rozszyfrować informację podane w treści zadania.
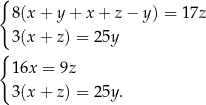
Z pierwszego równania mamy
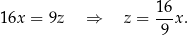
Podstawiamy to wyrażenie do drugiego równania.
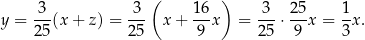
Teraz już jest łatwo, bo umiemy wyrazić długości wszystkich boków trójkąta 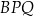 w zależności od
w zależności od  .
.
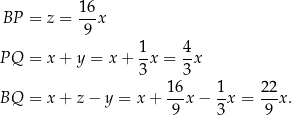
Najdłuższym bokiem trójkąta 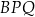 jest odcinek
jest odcinek 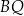 i
i
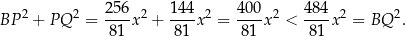
To oznacza, że trójkąt 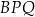 jest rozwartokątny (bo np. z tw cosinusów otrzymujemy wtedy, że
jest rozwartokątny (bo np. z tw cosinusów otrzymujemy wtedy, że 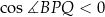 ).
).

