Zadanie nr 6587450

Wykaż, że odcinek łączący środki dwóch boków trójkąta jest równoległy do trzeciego boku i ma długość równą połowie tego boku.

Rozwiązanie

Szkicujemy trójkąt.

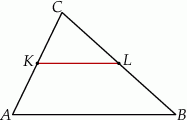
Sposób I

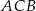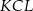Trójkąty ACB i KCL mają wspólny kąt przy wierzchołku 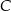, a długości boków przylegjących do tego kąta są proporcjonalne:

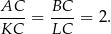
AC BC ---- = ----= 2. KC LC

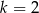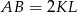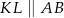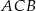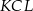W takim razie trójkąty te są podobne w skali k = 2 . To oznacza, że AB = 2KL oraz KL ∥ AB (bo trójkąty ACB i KCL jako podobne mają równe kąty).

Sposób II

Jeżeli oznaczymy przez 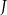jednokładność o środku 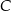i skali 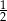1 2 , to

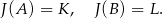
J(A ) = K, J(B) = L .

W takim razie

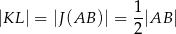
1 |KL | = |J(AB )| = --|AB | 2

oraz 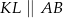KL ∥ AB .

Nie rozumiesz fragmentu rozwiązania?
W rozwiązaniu jest błąd lub literówka?
Masz inny pomysł na rozwiązanie tego zadania?
Napisz nam o tym!

Dodaj komentarz