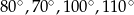/Szkoła średnia/Geometria/Planimetria/Trójkąt/Dowolny

Zadanie nr 6608228

Dodaj do ulubionych
Dodaj do rozwiązanych

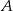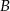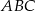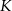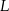Dwusieczne kątów A i B trójkąta ABC przecinają okrąg opisany na nim odpowiednio w punktach K i L . Oblicz miary kątów czworokąta 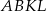ABKL wiedząc, że 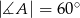|∡A | = 60∘ i |∡B | = 40∘ .

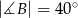Rozwiązanie

Zaczynamy od rysunku.

PIC

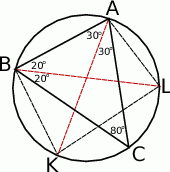
Korzystamy z tego, że trzeci kąt trójkąta 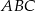ABC jest równy

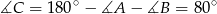
∡C = 180∘ − ∡A − ∡B = 80∘

oraz z równości kątów wpisanych opartych na tym samym łuku.

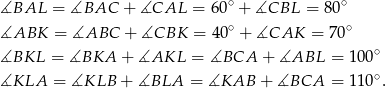
∘ ∘ ∡BAL = ∡BAC + ∡CAL = 6 0 + ∡CBL = 80 ∡ABK = ∡ABC + ∡CBK = 40∘ + ∡CAK = 70∘ ∘ ∡BKL = ∡BKA + ∡AKL = ∡BCA + ∡ABL = 10 0 ∡KLA = ∡KLB + ∡BLA = ∡KAB + ∡BCA = 11 0∘.

 
Odpowiedź: 80 ∘,70∘,100∘,11 0∘

Wersja PDF