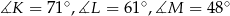/Szkoła średnia/Geometria/Planimetria/Trójkąt/Dowolny

Zadanie nr 6716027

Dodaj do ulubionych
Dodaj do rozwiązanych

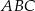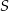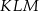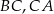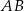W trójkącie ABC punkt S jest środkiem okręgu wpisanego, a punkty KLM są punktami styczności okręgu wpisanego w trójkąt z bokami BC ,CA i AB odpowiednio.

  • Uzasadnij, że na czworokącie 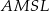AMSL można opisać okrąg.
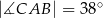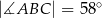  • Wiedząc, że ∘ |∡CAB | = 3 8 oraz ∘ |∡ABC | = 5 8 oblicz miary kątów trójkąta KLM .

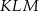Rozwiązanie

Rozpoczynamy od dużego rysunku.

PIC

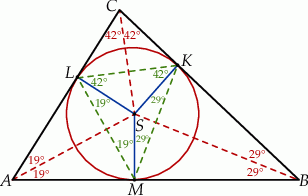
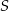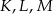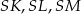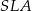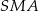  • Jeżeli połączymy środek okręgu wpisanego S z punktami styczności K ,L,M to odcinki SK ,SL,SM są prostopadłe do odpowiednich boków. W takim razie dwa przeciwległe kąty SLA i SMA czworokąta 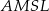AMSL są proste, czyli na czworokącie tym można opisać okrąg (co więcej średnicą tego okręgu jest AS ).
  •  

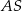    Sposób I

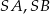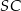    Ponieważ odcinki SA ,SB i SC są odcinkami dwusiecznych kątów wewnętrznych oraz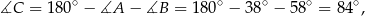

    ∡C = 180∘ − ∡A − ∡B = 180∘ − 38∘ − 58 ∘ = 84∘,

    mamy

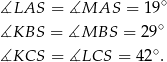
    ∡LAS = ∡MAS = 19∘ ∡KBS = ∡MBS = 2 9∘ ∡KCS = ∡LCS = 42∘.

    Ponieważ na czworokącie 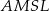AMSL można opisać okrąg, mamy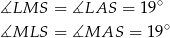

    ∘ ∡LMS = ∡LAS = 19 ∡MLS = ∡MAS = 19∘

    (kąty wpisane oparte na równych łukach).

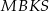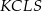    Ponadto, tak jak w poprzednim podpunkcie, uzasadniamy, że na czworokątach MBKS i KCLS można opisać okręgi. Stąd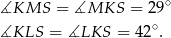

    ∡KMS = ∡MKS = 29∘ ∡KLS = ∡LKS = 42∘ .

    W takim razie miary kątów trójkąta 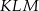KLM są równe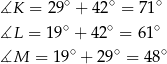

    ∡K = 29∘ + 42∘ = 71∘ ∘ ∘ ∘ ∡L = 19 + 4 2 = 61 ∡M = 19∘ + 29 ∘ = 48∘

Sposób II

Ponieważ dwa kąty czworokąta 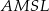AMSL są proste, mamy

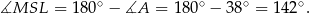
∘ ∘ ∘ ∘ ∡MSL = 180 − ∡A = 180 − 38 = 14 2 .

Teraz zauważmy, że trójkąt 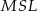MSL jest równoramienny, więc

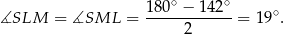
180∘ − 142∘ ∡SLM = ∡SML = ------------= 19∘. 2

Analogicznie uzasadniamy, że

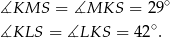
∡KMS = ∡MKS = 2 9∘ ∘ ∡KLS = ∡LKS = 42 .

Kąty trójkąta 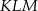KLM wyliczamy jak poprzednio.

Sposób III

Tak jak w poprzednim sposobie zauważamy, że 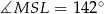∡MSL = 1 42∘ . Teraz zauważmy, że kąt 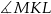∡MKL jest kątem wpisanym opartym na tym samym łuku, co kąt 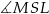∡MSL . Zatem

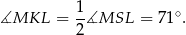
1 ∘ ∡MKL = -∡MSL = 71 . 2

Analogicznie obliczamy pozostałe kąty trójkąta 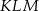KLM .  
Odpowiedź: ∘ ∘ ∘ ∡K = 71 ,∡L = 61 ,∡M = 48

Wersja PDF