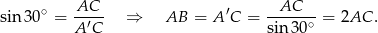Zadanie nr 6764676
W trójkącie  środkowa
środkowa  jest prostopadła do boku
jest prostopadła do boku  . Kąt
. Kąt 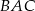 ma miarę
ma miarę 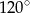 . Wykaż, że
. Wykaż, że 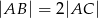 .
.
Rozwiązanie
Rozpoczynamy od rysunku.
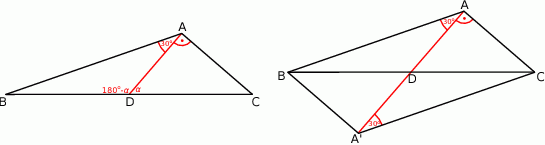
Sposób I
Oznaczmy 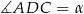 . Wtedy
. Wtedy 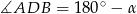 . Piszemy teraz twierdzenia sinusów w trójkątach
. Piszemy teraz twierdzenia sinusów w trójkątach 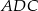 i
i 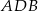 .
.
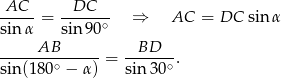
Ponieważ 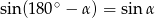 , drugą równość możemy zapisać w postaci
, drugą równość możemy zapisać w postaci
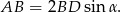
Mamy zatem
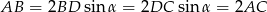
Sposób II
Tak jak poprzednio oznaczmy 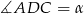 i niech
i niech 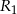 i
i 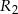 będą promieniami okręgów opisanych na trójkątach
będą promieniami okręgów opisanych na trójkątach 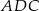 i
i 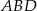 . Na mocy twierdzenia sinusów w tych trójkątach.
. Na mocy twierdzenia sinusów w tych trójkątach.
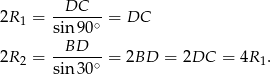
Zatem 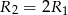 . Jeszcze raz zapisujemy twierdzenie sinusów w tych trójkątach, ale używamy teraz boków
. Jeszcze raz zapisujemy twierdzenie sinusów w tych trójkątach, ale używamy teraz boków 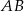 i
i 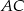 .
.
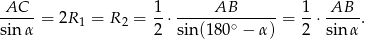
Zatem rzeczywiście 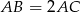 .
.
Sposób III
Niech 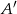 będzie odbiciem punktu
będzie odbiciem punktu 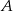 względem punktu
względem punktu 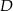 . Otrzymujemy w ten sposób równoległobok
. Otrzymujemy w ten sposób równoległobok 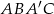 , w którym
, w którym 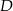 jest punktem przecięcia się przekątnych. Zauważmy, że
jest punktem przecięcia się przekątnych. Zauważmy, że 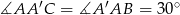 , więc w trójkącie prostokątnym
, więc w trójkącie prostokątnym 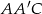 mamy
mamy