/Szkoła średnia/Geometria/Planimetria/Trójkąt/Dowolny

Zadanie nr 6899589

Dodaj do ulubionych
Dodaj do rozwiązanych

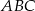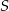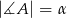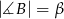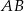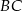Kąty ostre trójkąta ABC o polu S mają miary |∡A | = α , |∡B | = β . Oblicz długości boków AB i BC tego trójkąta.

Rozwiązanie

Rozpoczynamy od szkicowego rysunku.

PIC

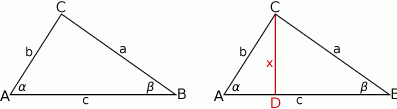
Sposób I

Ze wzoru na pole trójkąta z sinusem mamy

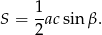
1 S = -ac sin β. 2

Z drugiej strony, na mocy twierdzenia sinusów mamy

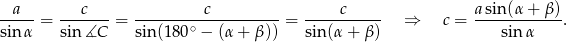
a c c c asin(α + β ) sinα- = sin-∡C- = sin-(180∘ −-(α+--β))-= sin-(α+--β)- ⇒ c = ----sin-α----.

Podstawiając to do poprzedniej równości mamy

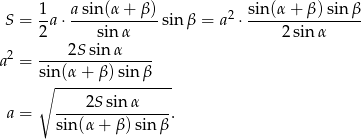
S = 1a ⋅ asin(α-+-β-)sin β = a2 ⋅ sin(α-+-β)-sin-β 2 sin α 2sin α 2 2Ssin α a = ---------------- ∘sin-(α+--β)sin-β--- 2S sin α a = ----------------. sin(α + β) sin β

Obliczamy c (ze wzoru otrzymanego na początku rozwiązania)

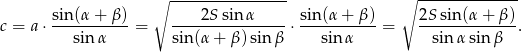
∘ ---------------- ∘ -------------- sin(α + β ) 2S sin α sin(α + β ) 2Ssin(α + β ) c = a⋅----------- = ----------------⋅-----------= -------------. sin α sin (α+ β) sin β sinα sin αsin β

Sposób II

Tym razem dorysujmy wysokość 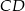CD i niech 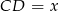CD = x . Mamy wtedy

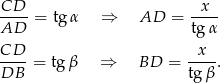
CD-- = tg α ⇒ AD = -x-- AD tgα CD x ----= tgβ ⇒ BD = ----. DB tg β

Korzystamy teraz z podanego pola.

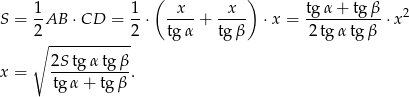
( ) S = 1AB ⋅CD = 1-⋅ -x--+ -x-- ⋅x = tg-α-+-tg-β-⋅x2 2 2 tgα tg β 2 tg α tg β ∘ ------------ x = 2S-tgα-tgβ-. tg α+ tg β

Mamy stąd

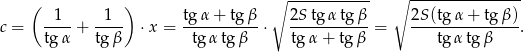
( ) ∘ ------------ ∘ ---------------- c = -1-- + -1-- ⋅x = tg-α+--tg-β-⋅ 2S-tg-α-tg-β-= 2S-(tgα-+-tg-β). tg α tg β tg αtg β tgα + tg β tgα tgβ

Długość boku 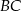BC obliczamy korzystając z twierdzenia Pitagorasa w trójkącie BDC .

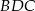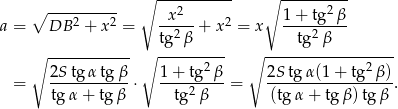
∘ ----------- ∘ ---------- ∘ ---------- x2 1 + tg2 β a = DB 2 + x2 = ---2- + x2 = x ----2---- tg β tg β ∘ ------------ ∘ -------2-- ∘ --------------2--- = 2Stg-αtg-β-⋅ 1+--tg--β-= 2S-tg-α(1+--tg--β)-. tgα + tg β tg 2β (tg α + tg β)tg β

 
Odpowiedź: 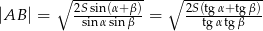∘ -2S-sin(α+β)- ∘ 2S(tgα+-tgβ)- |AB | = sinαsinβ = tgαtgβ , ∘ ------------- ∘ ------------ 2S tgα(1+tg2β) |BC | = sin2(αS+siβn)αsinβ-= -(tgα+-tgβ)tgβ-

Wersja PDF