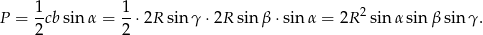/Szkoła średnia/Geometria/Planimetria/Trójkąt/Dowolny

Zadanie nr 7519997

Dodaj do ulubionych
Dodaj do rozwiązanych

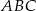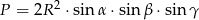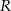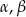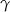Wykaż, że pole trójkąta ABC jest równe 2 P = 2R ⋅sin α ⋅sinβ ⋅sin γ , gdzie R jest promieniem okręgu opisanego na tym trójkącie, a α,β i γ są miarami kątów wewnętrznych tego trójkąta.

Rozwiązanie

Szkicujemy trójkąt.

PIC

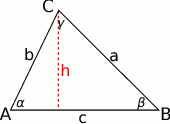
Wyprowadźmy najpierw znany wzór

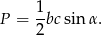
P = 1bc sin α. 2

W tym celu zauważmy, że

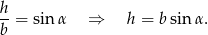
h --= sin α ⇒ h = bsinα . b

Mamy stąd

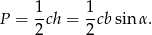
1 1 P = --ch = --cbsin α. 2 2

Jeżeli teraz skorzystamy z twierdzenia sinusów

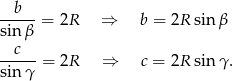
--b-- sin β = 2R ⇒ b = 2R sin β --c-- = 2R ⇒ c = 2R sin γ. sin γ

to mamy

1 1 P = -cb sin α = --⋅2R sin γ ⋅2R sin β ⋅sin α = 2R 2 sin α sin β sin γ. 2 2
Wersja PDF