Zadanie nr 7594797
Dany jest trójkąt 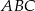 oraz punkt
oraz punkt 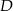 na jego boku
na jego boku 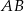 taki, że
taki, że 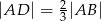 . Z wierzchołka
. Z wierzchołka 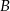 poprowadzono środkową
poprowadzono środkową 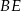 do boku
do boku 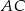 . Punkt
. Punkt 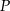 jest punktem wspólnym odcinków
jest punktem wspólnym odcinków 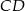 i
i 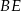 . Wykaż, że punkt
. Wykaż, że punkt 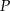 jest środkiem odcinka
jest środkiem odcinka 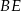 .
.
Rozwiązanie
Szkicujemy opisaną sytuację.
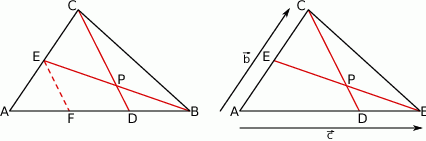
Sposób I
Niech 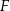 będzie takim punktem odcinka
będzie takim punktem odcinka 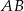 , że
, że 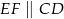 . Odcinek
. Odcinek 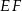 jest równoległy do podstawy
jest równoległy do podstawy 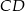 trójkąta
trójkąta 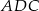 i przechodzi przez środek boku
i przechodzi przez środek boku 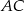 . Jest to więc odcinek łączący środki boków w trójkącie
. Jest to więc odcinek łączący środki boków w trójkącie 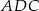 . W szczególności
. W szczególności
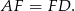
Z założenia wiemy ponadto, że 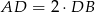 , czyli
, czyli
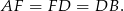
Patrzymy teraz na trójkąt 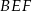 – w trójkącie tym odcinek
– w trójkącie tym odcinek 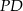 jest równoległy do podstawy
jest równoległy do podstawy 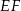 i przechodzi przez środek boku
i przechodzi przez środek boku 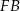 . Zatem (na mocy twierdzenia Talesa) jest to odcinek łączący środki boków w trójkącie
. Zatem (na mocy twierdzenia Talesa) jest to odcinek łączący środki boków w trójkącie 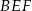 . W szczególności
. W szczególności
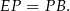
Sposób II
Tym razem skorzystamy z rachunku wektorowego. Oznaczmy 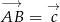 ,
, 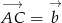 oraz
oraz 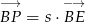 ,
, 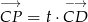 . Mamy zatem
. Mamy zatem
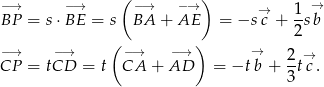
Z trójkąta 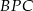 otrzymujemy.
otrzymujemy.
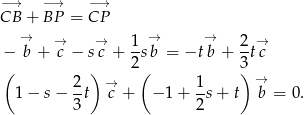
Wektory 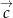 i
i 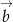 nie są równoległe, więc wyrażenia w obu nawiasach muszą być zerami. Mamy więc
nie są równoległe, więc wyrażenia w obu nawiasach muszą być zerami. Mamy więc
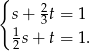
Podstawiając 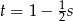 z drugiego równania do pierwszego mamy
z drugiego równania do pierwszego mamy
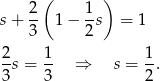
Zatem rzeczywiście