Zadanie nr 7613198
Dany jest trójkąt 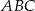 , w którym
, w którym 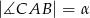 i
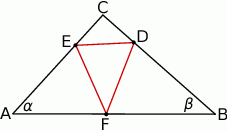
i 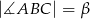 (zobacz rysunek). Na bokach
(zobacz rysunek). Na bokach 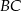 ,
, 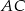 i
i 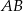 tego trójkąta wybrano odpowiednio punkty
tego trójkąta wybrano odpowiednio punkty 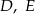 i
i 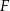 w taki sposób, że
w taki sposób, że 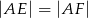 ,
, 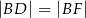 i
i 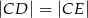 . Oblicz miary kątów trójkąta
. Oblicz miary kątów trójkąta 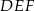 .
.
Rozwiązanie
Każdy z trójkątów 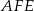 ,
, 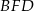 i
i 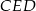 jest równoramienny, więc
jest równoramienny, więc
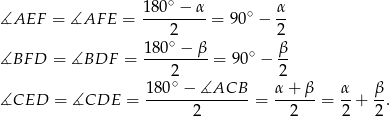
Stąd
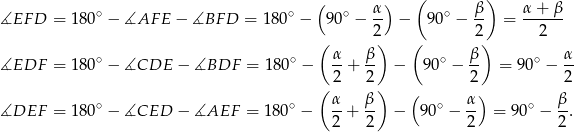
Odpowiedź: