/Szkoła średnia/Geometria/Planimetria/Trójkąt/Dowolny

Zadanie nr 7912169

Dodaj do ulubionych
Dodaj do rozwiązanych

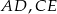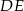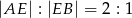Trójkąt podzielono odcinkami AD ,CE i DE na 5 trójkątów, przy czym |AE | : |EB | = 2 : 1 .

PIC

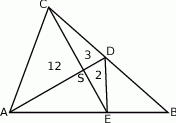
Korzystając z podanych pól trzech z tych trójkątów, wyznacz pole trójkąta 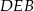DEB .

Rozwiązanie

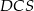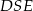Zauważmy, że trójkąty DCS i DSE mają wspólną wysokość opuszczoną na prostą 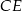CE , zatem stosunek ich pól jest równy stosunkowi ich podstaw. Zatem

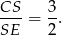
CS- = 3-. SE 2

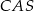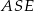Podobnie jest z trójkątami CAS i ASE , co pozwala wyliczyć pole trójkąta ASE .

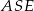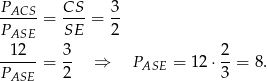
PACS- = CS- = 3- PASE SE 2 12 3 2 ----- = -- ⇒ PASE = 12 ⋅--= 8. PASE 2 3

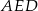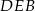Teraz patrzymy na trójkąty AED i DEB – mają wspólną wysokość opuszczoną na prostą 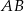AB oraz wiemy, że stosunek ich podstaw jest równy 2:1. Zatem

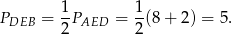
P = 1P = 1(8+ 2) = 5. DEB 2 AED 2

 
Odpowiedź: 5

Wersja PDF