/Szkoła średnia/Geometria/Planimetria/Trójkąt/Dowolny

Zadanie nr 8192673

Dodaj do ulubionych
Dodaj do rozwiązanych

Styczna w punkcie 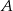A do okręgu opisanego na trójkącie 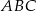ABC przecina prostą 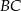BC w punkcie 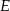E . Niech 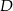D będzie punktem przecięcia dwusiecznej kąta 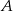A z prostą 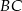BC . Udowodnić, że AE = ED .

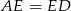Rozwiązanie

Oznaczmy 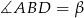∡ABD = β i ∡DAB = α .

PIC

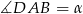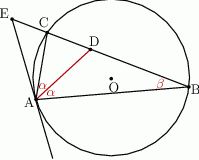
Suma kątów w trójkącie 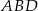ABD jest równa 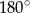18 0∘ , więc

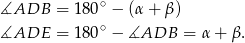
∘ ∡ADB = 18 0 − (α+ β) ∡ADE = 18 0∘ − ∡ADB = α+ β.

Na mocy twierdzenia o stycznej i siecznej,

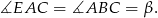
∡EAC = ∡ABC = β.

Stąd

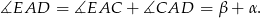
∡EAD = ∡EAC + ∡CAD = β + α.

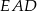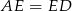To z oznacza, że trójkąt EAD jest równoramienny, czyli AE = ED .

Wersja PDF