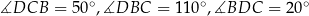/Szkoła średnia/Geometria/Planimetria/Trójkąt/Dowolny

Zadanie nr 8287402

Dodaj do ulubionych
Dodaj do rozwiązanych

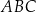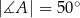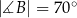W okrąg wpisano trójkąt ABC , w którym ∘ |∡A | = 50 i ∘ |∡B | = 70 . Przez wierzchołek kąta 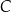C poprowadzono styczną do okręgu, przecinającą przedłużenie boku 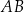AB w punkcie 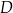D . Oblicz miary kątów trójkąta BCD .

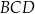Rozwiązanie

Zacznijmy od rysunku.

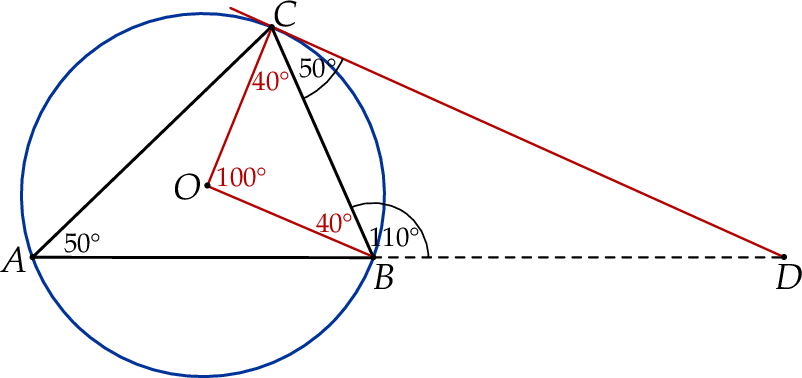
ZINFO-FIGURE

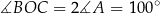Jeżeli połączymy środek okręgu z wierzchołkami B i C , to otrzymamy trójkąt równoramienny o kącie ∡BOC = 2 ∡A = 10 0∘ (kąty wpisany i środkowy oparte na wspólnej cięciwie). Zatem

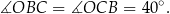
∘ ∡OBC = ∡OCB = 40 .

Ponieważ promień 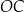OC jest prostopadły do stycznej 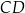CD , mamy

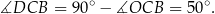
∘ ∘ ∡DCB = 90 − ∡OCB = 50 .

Ponadto

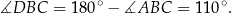
∡DBC = 180∘ − ∡ABC = 110∘.

Stąd

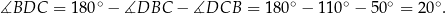
∡BDC = 180 ∘ − ∡DBC − ∡DCB = 180∘ − 110∘ − 50 ∘ = 20∘.

 
Odpowiedź: ∡DCB = 50∘,∡DBC = 110 ∘,∡BDC = 2 0∘

Wersja PDF