/Szkoła średnia/Geometria/Planimetria/Trójkąt/Dowolny

Zadanie nr 8859077

Dodaj do ulubionych
Dodaj do rozwiązanych

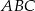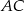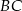W trójkącie ostrokątnym ABC , którego pole równa się 16, boki AC i BC mają długości 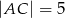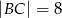|AC | = 5 , |BC | = 8 . Oblicz długość boku AB .

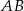Rozwiązanie

Zaczynamy od rysunku.

PIC

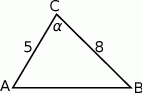
Znając dwa boki i pole możemy łatwo wyliczyć sinus kąta między tymi bokami.

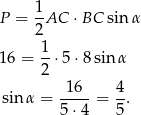
P = 1-AC ⋅ BC sinα 2 1 16 = --⋅5 ⋅8sin α 2 sin α = 1-6-= 4-. 5⋅4 5

Skoro wiemy, że trójkąt jest ostrokątny, to 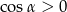co sα > 0 i możemy go wyliczyć z jedynki trygonometrycznej.

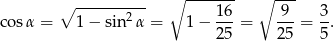
∘ ---------- ∘ ------- ∘ --- 2 16- -9- 3- cos α = 1− sin α = 1− 25 = 25 = 5.

Teraz wyliczymy długość trzeciego boku z twierdzenia cosinusów.

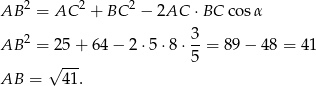
AB 2 = AC 2 + BC 2 − 2AC ⋅BC co sα 3 AB 2 = 25+ 64− 2⋅ 5⋅8 ⋅--= 89 − 48 = 4 1 √ --- 5 AB = 41.

 
Odpowiedź: AB = √ 41-

Wersja PDF