/Szkoła średnia/Geometria/Planimetria/Trójkąt/Dowolny

Zadanie nr 8946077

Dodaj do ulubionych
Dodaj do rozwiązanych

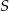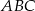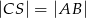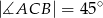Punkt S jest punktem przecięcia się wysokości trójkąta ostrokątnego ABC . Wykaż, że jeżeli |CS | = |AB | to |∡ACB | = 45∘ .

Rozwiązanie

Rozpoczynamy od rysunku.

PIC

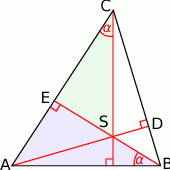
Zauważmy, że

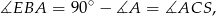
∡EBA = 90∘ − ∡A = ∡ACS ,

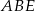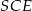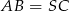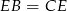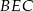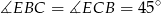czyli trójkąty ABE i SCE są prostokątne i mają równe kąty. Są więc podobne. Ponadto z założenia mają równe przeciwprostokątne AB = SC , więc są przystające. To oznacza, że EB = CE , czyli trójkąt prostokątny BEC jest równoramienny. Wówczas ∘ ∡EBC = ∡ECB = 45 .

Wersja PDF