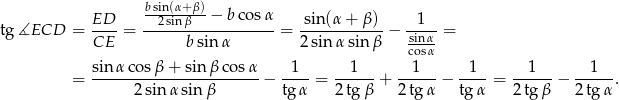/Szkoła średnia/Geometria/Planimetria/Trójkąt/Dowolny

Zadanie nr 9075575

Dodaj do ulubionych
Dodaj do rozwiązanych

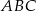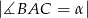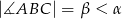W trójkącie ostrokątnym ABC dane są |∡BAC = α| i |∡ABC | = β < α . Wykaż, że tangens kąta utworzonego przez środkową i wysokość opuszczone z wierzchołka 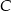C jest równy

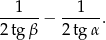
--1---− --1---. 2tg β 2 tgα

Rozwiązanie

Szkicujemy opisaną sytuację.

PIC

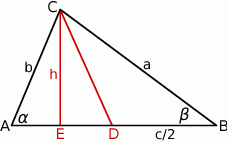
W trójkącie prostokątnym 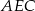AEC mamy

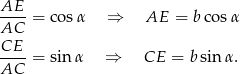
AE--= cosα ⇒ AE = b cosα AC CE-- AC = sin α ⇒ CE = bsinα .

Spróbujemy teraz obliczyć długość boku 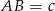AB = c w zależności od 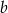b i podanych kątów. Korzystamy z twierdzenia sinusów.

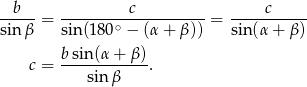
--b-- ----------c--------- ----c------ sinβ = sin(18 0∘ − (α+ β)) = sin (α+ β) c = b-sin-(α-+-β). sinβ

Stąd

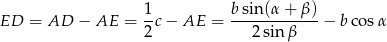
1- b-sin-(α+--β) ED = AD − AE = 2 c− AE = 2 sin β − b cosα

i

bsin(α+β)- ED-- --2-sinβ--−--bco-sα sin(α-+-β-)- --1-- tg∡ECD = CE = b sin α = 2sin αsin β − sinα-= cosα sin-αco-sβ-+-sinβ-cos-α --1- --1--- --1--- -1-- --1--- --1--- = 2 sin α sin β − tg α = 2tg β + 2 tg α − tg α = 2tg β − 2 tgα .
Wersja PDF