Zadanie nr 9203003

Na boku 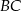trójkąta 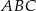ABC wybrano punkt 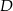tak, by 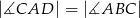|∡CAD | = |∡ABC | . Odcinek 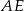jest dwusieczną kąta 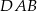DAB . Udowodnij, że |CE | = |AC | .

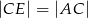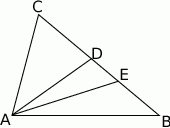
Rozwiązanie

Zaczynamy od zaznaczenia na rysunku podanych informacji.

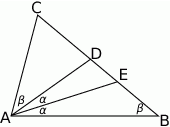
Mamy udowodnić, że trójkąt 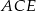ACE jest równoramienny, a dokładniej, że jego kąty przy podstawie 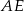są równe. Mamy

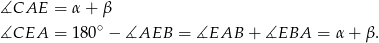
∡CAE = α + β ∡CEA = 180∘ − ∡AEB = ∡EAB + ∡EBA = α + β.

W przedostatniej równości, patrzyliśmy na sumę kątów w trójkącie 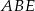ABE .

Nie rozumiesz fragmentu rozwiązania?
W rozwiązaniu jest błąd lub literówka?
Masz inny pomysł na rozwiązanie tego zadania?
Napisz nam o tym!

Dodaj komentarz