/Szkoła średnia/Geometria/Planimetria/Trójkąt/Dowolny

Zadanie nr 9399544

Dodaj do ulubionych
Dodaj do rozwiązanych

Pole trójkąta rozwartokątnego jest równe 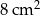2 8 cm . Dwa boki tego trójkąta mają długości 4 cm i 5 cm. Oblicz długość trzeciego boku tego trójkąta.

Rozwiązanie

Zacznijmy od schematycznego rysunku.

PIC

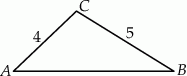
Mając dwa boki i pole, możemy łatwo obliczyć sinus kąta między tymi bokami. Potem długość trzeciego boku obliczymy z twierdzenia cosinusów. Ze wzoru na pole z sinusem mamy

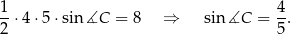
1- 4- 2 ⋅4 ⋅5⋅ sin ∡C = 8 ⇒ sin∡C = 5 .

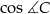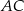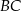Obliczmy teraz co s∡C . Gdybyśmy wiedzieli, że kąt rozwarty jest między bokami AC i BC to byśmy wiedzieli, że 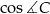cos∡C jest ujemny i byłoby łatwiej. Ponieważ jednak tego nie wiemy, musimy rozważyć dwie możliwości

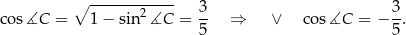
∘ ------------ 3 3 cos ∡C = 1 − sin2 ∡C = -- ⇒ ∨ cos∡C = − -. 5 5

Obliczmy długość boku 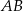AB w obu przypadkach.

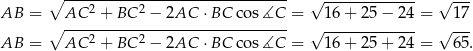
∘ ----2-----2-------------------- √ ------------- √ --- AB = ∘ AC---+-BC---−-2AC--⋅BC--cos∡C--= 16-+-25-−-24-= √ 17- AB = AC 2 + BC 2 − 2AC ⋅BC cos∡C = √ 16 + 25 + 24 = 65.

Zauważmy, że w pierwszym przypadku

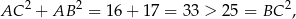
AC 2 + AB 2 = 16 + 17 = 33 > 25 = BC 2,

czyli na mocy twierdzenia cosinusów, kąt przy wierzchołku 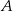A jest ostry, czyli wszystkie kąty są ostre, bo ten jest największy (leży naprzeciwko najdłuższego boku).  
Odpowiedź: √ --- 65 cm

Wersja PDF