/Szkoła średnia/Geometria/Planimetria/Trójkąt/Dowolny

Zadanie nr 9721850

Dodaj do ulubionych
Dodaj do rozwiązanych

Uzasadnij, że jeżeli dwie dwusieczne trójkąta przecinają się pod kątem 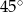∘ 45 to trójkąt jest prostokątny.

Rozwiązanie

Robimy rysunek.

PIC

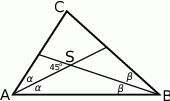
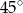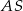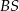Pierwszy problem jaki napotykamy, to gdzie zaznaczyć podany kąt 45∘ ? – są dwa kąty między prostymi AS i BS (w sumie dają 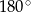1 80∘ ) i musimy wiedzieć, o który z nich chodzi. Ponieważ jednak

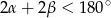
2α + 2 β < 180 ∘

(suma dwóch kątów w trójkącie), więc 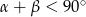α + β < 90∘ , czyli kąt

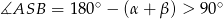
∘ ∘ ∡ASB = 180 − (α + β ) > 90

jest na pewno rozwarty. Zatem 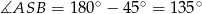∘ ∘ ∘ ∡ASB = 180 − 45 = 135 i korzystając z powyższej równości mamy

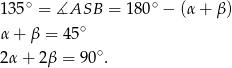
∘ ∘ 135 = ∡ASB = 18 0 − (α + β) α + β = 45∘ ∘ 2α + 2β = 90 .

Zatem 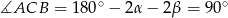∘ ∘ ∡ACB = 180 − 2α − 2β = 90 .

Wersja PDF