/Szkoła średnia/Geometria/Stereometria/Walec

Zadanie nr 5371921

Powierzchnia boczna walca po rozwinięciu na płaszczyznę jest prostokątem. Przekątna tego prostokąta ma długość 12 i tworzy z bokiem, którego długość jest równa wysokości walca, kąt o mierze 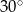30∘ .

  • Oblicz pole powierzchni bocznej tego walca.
  • Sprawdź, czy objętość tego walca jest większa od 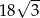√ -- 18 3 . Odpowiedź uzasadnij.
Wersja PDF

Rozwiązanie

Zaczynamy od schematycznego rysunku.

PIC

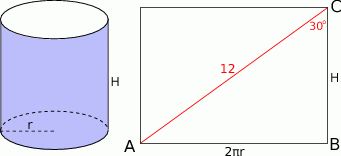
Przy oznaczeniach z rysunku mamy

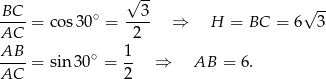
√ -- BC--= cos30 ∘ = --3- ⇒ H = BC = 6√ 3- AC 2 AB ∘ 1 ----= sin 30 = -- ⇒ AB = 6. AC 2

Poziomy bok prostokąta jest ponadto równy obwodowi okręgu w podstawie walca, czyli

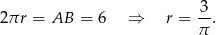
3 2πr = AB = 6 ⇒ r = --. π
  • Liczymy teraz pole powierzchni bocznej.
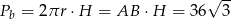
    √ -- Pb = 2πr ⋅ H = AB ⋅ H = 36 3

     
    Odpowiedź: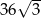 √ -- 36 3

  • Liczymy objętość
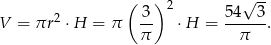
    ( ) 2 √ -- V = πr 2 ⋅H = π -3 ⋅H = 54--3-. π π

    Pozostało sprawdzić, czy prawdą jest, że

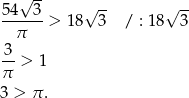
    √ -- √ -- √ -- 54--3-> 18 3 / : 18 3 π 3 π-> 1 3 > π .

    Ta nierówność jest oczywiście nieprawdziwa, więc wyjściowa też nie może być prawdziwa.  
    Odpowiedź: Nie, nie jest prawdziwa.

Wersja PDF